Sử dụng tính chất hai góc kề một đáy của hình thang có tổng bằng \(180^\circ \). Hướng dẫn giải Giải bài 3.8 trang 34 sách bài tập toán 8 – Kết nối tri thức với cuộc sống – Bài 11. Hình thang cân. Chứng minh rằng trong hình thang có nhiều nhất hai góc tù….
Đề bài/câu hỏi:
Chứng minh rằng trong hình thang có nhiều nhất hai góc tù.
Hướng dẫn:
Sử dụng tính chất hai góc kề một đáy của hình thang có tổng bằng \(180^\circ \).
Lời giải:
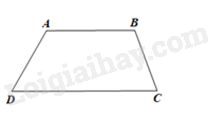
Xét hình thang ABCD có AB // CD
Ta có:
- \(\widehat A\) và \(\widehat D\) là hai góc kề với cạnh bên AD
Suy ra \(\widehat A + \widehat D = 180^\circ \) nên trong hai góc đó có nhiều nhất 1 góc tù.
- \(\widehat B\) và \(\widehat C\) là hai góc kề với cạnh bên BC
Suy ra \(\widehat B + \widehat C = 180^\circ \) nên trong hai góc đó có nhiều nhất 1 góc tù.
Do đó trong bốn góc \(\widehat A;\widehat B;\widehat C;\widehat D\)có nhiều nhất hai góc tù.