Sử dụng tính chất của hình vuông để tính. Hướng dẫn giải Giải bài 3.26 trang 42 sách bài tập toán 8 – Kết nối tri thức với cuộc sống – Bài 14. Hình thoi và hình vuông. Cho hình vuông ABCD với tâm O và có cạnh bằng 2cm. Hai tia Ox, Oy tạo thành góc vuông….
Đề bài/câu hỏi:
Cho hình vuông ABCD với tâm O và có cạnh bằng 2cm. Hai tia Ox, Oy tạo thành góc vuông. Tính diện tích của phần hình vuông nằm bên trong góc xOy.
Hướng dẫn:
Sử dụng tính chất của hình vuông để tính: Hình vuông có hai đường chéo vuông góc với nhau và là các đường phân giác của các góc của hình vuông.
Lời giải:
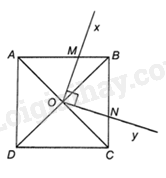
Tia Ox phải cắt một cạnh của hình vuông ABCD. Giả sử Ox cắt cạnh AB tại M.
+ Khi M trùng A hay B thì tia Oy phải đi qua một đỉnh của hình vuông và dễ thấy phần hình vuông nằm trong góc xOy là một phần tư của hình vuông.
+ Khi M nằm giữa A và B thì tia Oy phải cắt cạnh BC hoặc cạnh AD; giả sử tia Oy cắt BC tại N thì N nằm giữa B và C.
Do ABCD là hình vuông nên AC và BD là các đường phân giác của các góc của hình vuông, \(AC \bot BD\) tại O, \(OA = OB\)
Ta có: \(\widehat {MAO} = \widehat {NBO}\left( { = {{90}^0} – \widehat {MBO}} \right)\)
Mà \(\widehat {MOA} + \widehat {MOB} = \widehat {NOB} + \widehat {MOB}\left( { = {{90}^0}} \right)\) nên \(\widehat {MOA} = \widehat {NOB}\)
Tam giác OAM và tam giác OBN có:
\(\widehat {MAO} = \widehat {NBO}\) (cmt), \(OA = OB\)(cmt), \(\widehat {MOA} = \widehat {NOB}\)(cmt)
Do đó, \(\Delta OAM = \Delta OBN\left( {g – c – g} \right)\) nên hai tam giác này có cùng diện tích.
Ta có: Diện tích của phần hình vuông nằm trong góc xOy là diện tích tứ giác OMBN.
Mà \({S_{OMBN}} = {S_{OBM}} + {S_{OBN}};{S_{AOB}} = {S_{OAM}} + {S_{OBM}}\) nên \({S_{OMBN}} = {S_{AOB}}\)
Do đó, diện tích phần hình vuông nằm trong góc xOy bằng \(\frac{1}{4}\) diện tích hình vuông ABCD.
Tương tự khi N nằm giữa A và D thì diện tích của phần hình vuông nằm trong góc xOy bằng \(\frac{1}{4}\) diện tích hình vuông ABCD.
Vậy diện tích cần tìm là: \(\frac{1}{4}{.2^2} = 1\left( {c{m^2}} \right)\)