Sử dụng kiến thức dấu hiệu nhận biết hình bình hành để chứng minh. Hướng dẫn trả lời Giải bài 3.17 trang 37 sách bài tập toán 8 – Kết nối tri thức với cuộc sống – Bài 12. Hình bình hành. Cho hai điểm phân biệt A, B nằm bên trong góc xOy (không bẹt). Tìm điểm D thuộc tia Ox,…
Đề bài/câu hỏi:
Cho hai điểm phân biệt A, B nằm bên trong góc xOy (không bẹt). Tìm điểm D thuộc tia Ox, điểm E thuộc tia Oy sao cho ADBE là một hình bình hành.
Hướng dẫn:
Sử dụng kiến thức dấu hiệu nhận biết hình bình hành để chứng minh: Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Lời giải:
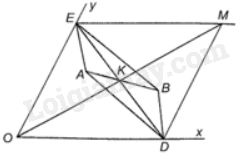
Gọi K là trung điểm của AB thì điểm cần tìm D thuộc Ox, E cần tìm thuộc Oy sao cho K là trung điểm của DE.
Lấy điểm M sao cho K là trung điểm của OM, qua M kẻ đường thẳng song song với Ox cắt Oy tại E, và đường thẳng song song với Oy cắt Ox ở D. Khi đó, D, E xác định như trên là các điểm cần tìm.
Thậy vậy, nếu ME//OD, MD//OE thì ODME là hình bình hành. Mà K là trung điểm của OM nên K là trung điểm của DE.
Tứ giác AEBD có: K là trung điểm của DE, K là trung điểm của AB, AB và ED cắt nhau tại K nên tứ giác AEBD là hình bình hành.