Sử dụng kiến thức về thể tích của hình chóp tam giác đều để tính thể tích hình chóp tam giác đều S. MNP. Lời giải Giải bài 10.7 trang 73 sách bài tập toán 8 – Kết nối tri thức với cuộc sống – Bài 38. Hình chóp tam giác đều. Cho hình chóp tam giác đều S.MNP có cạnh đáy bằng 8cm, đường cao bằng 6cm (H.10.8)….
Đề bài/câu hỏi:
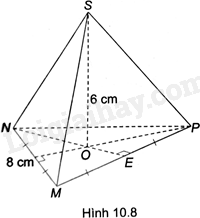
Cho hình chóp tam giác đều S.MNP có cạnh đáy bằng 8cm, đường cao bằng 6cm (H.10.8). Hãy tính thể tích của hình chóp S.MNP. Cho biết $\sqrt{48}\approx 6,9$
Hướng dẫn:
Sử dụng kiến thức về thể tích của hình chóp tam giác đều để tính thể tích hình chóp tam giác đều S. MNP: Thể tích của hình chóp tam giác đều bằng $\frac{1}{3}$ tích của diện tích đáy với chiều cao của nó.
Lời giải:
Gọi NE là đường trung tuyến của tam giác MNP và O là giao điểm của hai đường trung tuyến trong tam giác MNP. Do đó SO là chiều cao của hình chóp nên $SO=6cm$
Tam giác MNP là tam giác đều nên NE là đường trung tuyến đồng thời là đường cao. Do đó, $ME=EP=\frac{1}{2}MP=4\left( cm \right)$
Tam giác MEN vuông tại E nên $M{{E}^{2}}+N{{E}^{2}}=M{{N}^{2}}$ (định lí Pythagore)
$N{{E}^{2}}=64-16=48$ nên $NE=\sqrt{48}\approx 6,9\left( cm \right)$
Thể tích của hình chóp S.MNP là:
$V=\frac{1}{3}{{S}_{MNE}}.SO=\frac{1}{3}.\frac{1}{2}.MN.NE.SO=\frac{1}{6}.8.6,9.6=55,2\left( c{{m}^{3}} \right)$