Sử dụng kiến thức về tính chất hình bình hành để chứng minh. Hướng dẫn giải Giải bài 8 trang 65 sách bài tập toán 8 – Chân trời sáng tạo – Bài 4. Hình bình hành – Hình thoi. Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O….
Đề bài/câu hỏi:
Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Gọi M và N lần lượt là trung điểm của OB và OD. Chứng minh tứ giác AMCN là hình bình hành.
Hướng dẫn:
+ Sử dụng kiến thức về tính chất hình bình hành để chứng minh: Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
+ Sử dụng kiến thức về dấu hiệu nhận biết hình bình hành để chứng minh: Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Lời giải:
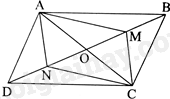
Tứ giác ABCD là hình bình hành nên \(OA = OC\), \(OB = OD\)
Mà: \(ON = \frac{1}{2}OD\) (do N là trung điểm của OD)
\(OM = \frac{1}{2}OB\) (do M là trung điểm của OB)
Do đó, \(OM = ON\)
Tứ giác AMCN có: \(OM = ON\) (cmt), \(OA = OC\) (cmt) nên tứ giác AMCN là hình bình hành.