Sử dụng dấu hiệu nhận biết hình bình hành để chứng minh. Hướng dẫn cách giải/trả lời Giải bài 7 trang 65 sách bài tập toán 8 – Chân trời sáng tạo – Bài 4. Hình bình hành – Hình thoi. Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA….
Đề bài/câu hỏi:
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA. Chứng minh rằng tứ giác MNPQ là hình bình hành.
Hướng dẫn:
Sử dụng dấu hiệu nhận biết hình bình hành để chứng minh: Tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành.
Lời giải:
Xét bài toán phụ: Cho tam giác ABC có M, N lần lượt là trung điểm của cạnh AB, AC. Lấy P đối xứng với M qua N. Chứng minh rằng MN//BC, \(MN = \frac{{BC}}{2}\)
Chứng minh:
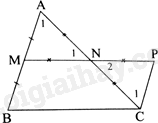
Tam giác AMN và tam giác CPN có:
\(NA = NC\left( {gt} \right),\widehat {{N_1}} = \widehat {{N_2}}\) (hai góc đối đỉnh), \(NM = NP\) (gt)
Do đó, \(\Delta ANM = \Delta CNP\left( {c – g – c} \right)\)
Suy ra \(\widehat {{A_1}} = \widehat {{C_1}}\), mà hai góc này ở vị trí so le trong nên CP//AB hay CP//BM
Lại có: \(CP = AM = BM\)
Tứ giác BMPC có: CP//BM, \(CP = BM\) nên tứ giác BMPC là hình bình hành. Do đó, MN//BC, \(MN = \frac{{BC}}{2}\)
Giải bài 7
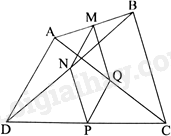
Xét tam giác ABD có M, N lần lượt là trung điểm của AB, BD (giả thiết) nên theo bài toán phụ, ta có: \(MN = \frac{{AD}}{2}\), MN//AD.
Xét tam giác ACD có P, Q lần lượt là trung điểm của DC, AC (giả thiết) nên theo bài toán phụ, ta có: \(PQ = \frac{{AD}}{2}\), PQ//AD.
Xét tứ giác MNPQ có MN//PQ (cùng song song với AD), \(MN = PQ\left( { = \frac{{AD}}{2}} \right)\) nên tứ giác MNPQ là hình bình hành.