Sử dụng kiến thức về đường chéo trong tứ giác: Trong tứ giác, đường chéo là đoạn thẳng nối hai đỉnh đối nhau. Phân tích và giải Giải bài 8 trang 57 sách bài tập toán 8 – Chân trời sáng tạo – Bài 2. Tứ giác. Chứng minh rằng trong một tứ giác,…
Đề bài/câu hỏi:
Chứng minh rằng trong một tứ giác, tổng độ dài hai đường chéo lớn hơn nửa chu vi tứ giác đó.
Hướng dẫn:
+ Sử dụng kiến thức về đường chéo trong tứ giác: Trong tứ giác, đường chéo là đoạn thẳng nối hai đỉnh đối nhau.
+ Sử dụng kiến thức về bất đẳng thức trong tam giác để chứng minh: Trong một tam giác, tổng độ dài hai cạnh tam giác lớn hơn độ dài cạnh còn lại.
Lời giải:
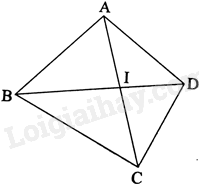
Vẽ tứ giác ABCD có I là giao điểm của hai đường chéo AC và BD.
Theo bất đẳng thức trong tam giác, ta có:
\(IA + IB > AB\), \(IB + IC > BC\), \(IC + ID > CB\), \(IA + ID > AD\)
Do đó: \(2\left( {IA + IB + IC + ID} \right) > AB + BC + CD + DA\)
Hay \(2\left( {AC + BD} \right) > AB + BC + CD + DA\)
Do đó: \(AC + BD > \frac{{AB + BC + CD + DA}}{2}\) (đpcm)