Sử dụng kiến thức về đường chéo của tứ giác: Trong tứ giác, đường chéo là đoạn thẳng nối hai đỉnh đối nhau. Hướng dẫn cách giải/trả lời Giải bài 7 trang 57 sách bài tập toán 8 – Chân trời sáng tạo – Bài 2. Tứ giác. Cho tứ giác ABCD có hai đường chéo vuông góc với nhau tại I. Cho biết (BC = 15cm,…
Đề bài/câu hỏi:
Cho tứ giác ABCD có hai đường chéo vuông góc với nhau tại I. Cho biết \(BC = 15cm,CD = 24cm\) và \(AD = 20cm.\) Tính độ dài AB.
Hướng dẫn:
+ Sử dụng kiến thức về đường chéo của tứ giác: Trong tứ giác, đường chéo là đoạn thẳng nối hai đỉnh đối nhau.
+ Sử dụng kiến thức về định lí Pythagore vào tam giác vuông: Trong một tam giác vuông, bình vuông độ dài của cạnh huyền bằng tổng các bình phương độ dài của hai cạnh góc vuông.
Lời giải:
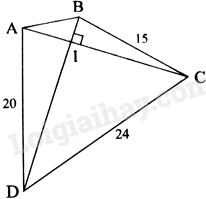
Áp dụng định lí Pythagore vào tam giác AIB vuông tại I ta có: \(I{A^2} + I{B^2} = A{B^2}\)
Áp dụng định lí Pythagore vào tam giác CIB vuông tại I ta có: \(I{C^2} + I{B^2} = B{C^2}\)
Áp dụng định lí Pythagore vào tam giác AID vuông tại I ta có: \(I{A^2} + I{D^2} = A{D^2}\)
Áp dụng định lí Pythagore vào tam giác CID vuông tại I ta có: \(I{C^2} + I{D^2} = C{D^2}\)
Do đó: \(A{B^2} + C{D^2} = \left( {I{A^2} + I{D^2}} \right) + \left( {I{C^2} + I{B^2}} \right)\)
\(A{B^2} + C{D^2} = A{D^2} + B{C^2}\)
\(A{B^2} = A{D^2} + B{C^2} – C{D^2} = {20^2} + {15^2} – {24^2} = 49\)
Do đó, \(AB = 7cm\)