Bài 6 trang 75 SBT toán 8 – Chân trời sáng tạo tập 2: Cho tam giác ABC vuông tại A AB < AC , M là điểm bất kì trên cạnh AC. Kẻ MD ⊥ BC D ∈ BC

Đề bài/câu hỏi:

Cho tam giác ABC vuông tại A \(\left( {AB < AC} \right)\), M là điểm bất kì trên cạnh AC. Kẻ \(MD \bot BC\left( {D \in BC} \right)\).

a) Chứng minh rằng $\Delta DMC\backsim \Delta ABC$.

b) Gọi E là giao điểm của đường thẳng AB và đường thẳng MD. Chứng minh rằng \(DB.DC = DE.DM\)

c) Đường thẳng BM cắt EC tại K. Chứng minh rằng \(\widehat {EKA} = \widehat {EBC}\).

Hướng dẫn:

+ Sử dụng kiến thức về trường hợp đồng dạng thứ ba của hai tam giác (g.g) để tính: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

+ Sử dụng kiến thức về trường hợp đồng dạng thứ hai của hai tam giác (c.g.c) để tính chứng minh: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng với nhau.

Lời giải:

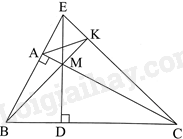
a) Tam giác DMC và tam giác ABC có:

\(\widehat {MDC} = \widehat {BAC} = {90^0},\widehat {ACB}\;chung\)

Do đó, $\Delta DMC\backsim \Delta ABC\left( g.g \right)$

b) Tam giác DBE và tam giác DMC có:

\(\widehat {BDE} = \widehat {MDC} = {90^0},\widehat {DEB} = \widehat {DCM}\) (cùng phụ với góc ABC)

Suy ra \(\Delta DBE\backsim \Delta DMC\left( g.g \right)\)

Suy ra: \(\frac{{DB}}{{DM}} = \frac{{DE}}{{DC}}\), nên \(DB.DC = DE.DM\)

c) Tam giác EBC có hai đường cao ED và CA cắt nhau tại M nên M là trực tâm của tam giác EBC. Do đó, \(BK \bot EC\)

Tam giác EAC và tam giác EKB có:

\(\widehat {EAC} = \widehat {EKB} = {90^0},\widehat {BEC}\;chung\)

Do đó, $\Delta EAC\backsim \Delta EKB\left( g.g \right)$nên \(\frac{{EA}}{{EK}} = \frac{{EC}}{{EB}}\), hay \(\frac{{EA}}{{EC}} = \frac{{EK}}{{EB}}\)

Tam giác EAK và tam giác ECB có: \(\frac{{EA}}{{EC}} = \frac{{EK}}{{EB}}\), góc BEC chung. Do đó, $\Delta EAK\backsim \Delta ECB\left( c.g.c \right)$ nên \(\widehat {EKA} = \widehat {EBC}\)