Sử dụng kiến thức về trường hợp đồng dạng thứ ba của hai tam giác (g. g) để tính. Hướng dẫn giải Giải bài 5 trang 75 sách bài tập toán 8 – Chân trời sáng tạo tập 2 – Bài tập cuối chương 8. Một người dùng thước êke để đo chiều cao từ chân đến mắt người đó là 1,…
Đề bài/câu hỏi:
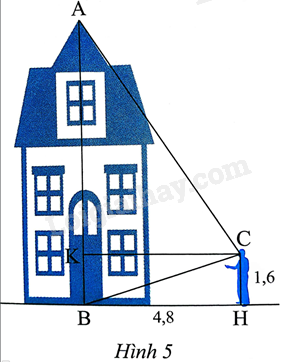
Một người dùng thước êke để đo chiều cao từ chân đến mắt người đó là 1,6m và đứng cách trục chính tòa nhà 4,8m (Hình 5). Hỏi tòa nhà cao khoảng bao nhiêu?
Hướng dẫn:
Sử dụng kiến thức về trường hợp đồng dạng thứ ba của hai tam giác (g.g) để tính: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải:
Ta có: \(\widehat A = \widehat {BCK}\) (cùng phụ với góc KCA).
Lại có: KC//BH (cùng vuông góc với KB) nên \(\widehat {BCK} = \widehat {CBH}\) (hai góc so le trong)
Do đó, \(\widehat A = \widehat {HBC}\)
Tam giác AKC và tam giác BHC có: \(\widehat {AKC} = \widehat {BHC} = {90^0},\widehat A = \widehat {HBC}\) (cmt)
Do đó, $\Delta AKC\backsim \Delta BHC\left( g.g \right)$, suy ra \(\frac{{AK}}{{BH}} = \frac{{CK}}{{HC}}\), hay \(\frac{{AK}}{{4,8}} = \frac{{4,8}}{{1,6}}\)
Do đó, \(AK = \frac{{4,8.4,8}}{{1,6}} = 14,4\left( m \right)\). Vậy độ cao của tòa nhà là: \(14,4 + 1,6 = 16\left( m \right)\)