Áp dụng trường hợp đồng dạng thứ ba: góc – góc Nếu hai góc của tam giác này lần lượt bằng hai góc của tam. Trả lời Giải bài 49 trang 79 sách bài tập toán 8 – Cánh diều – Bài 8. Trường hợp đồng dạng thứ ba của tam giác. Cho hình vuông \(ABCD\), gọi \(O\) là giao điểm của hai đường chéo, lấy \(G\) trên cạnh \(BC\), \(H\…
Đề bài/câu hỏi:
Cho hình vuông \(ABCD\), gọi \(O\) là giao điểm của hai đường chéo, lấy \(G\) trên cạnh \(BC\), \(H\) trên cạnh \(CD\) sao cho \(\widehat {GOH} = 45^\circ \). Gọi \(M\) là trung điểm của \(AB\). Chứng minh:
a) \(\Delta HOD\backsim \Delta OGB\)
b) \(MG//AH\)
Hướng dẫn:
Áp dụng trường hợp đồng dạng thứ ba: góc – góc
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
Áp dụng trường hợp đồng dạng thứ ba của tam giác vào tam giác vuông:
Nếu tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Lời giải:
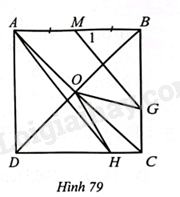
a) Ta có: \(\widehat {CDB} = \widehat {CBD} = 45^\circ \)
Mặt khác: \(\widehat {DOH} + \widehat {BOG} = 180^\circ – 45^\circ = 135^\circ ;\widehat {BOG} + \widehat {BGO} = 180^\circ – 45^\circ = 135^\circ \)
\( = > \widehat {DOH} = \widehat {BGO}\), do đó \(\Delta HOD\backsim \Delta OGB\).
b) Theo câu a, ta có
Đặt \(MB = a,AD = 2a\)
\( = > HD.GB = OB.OD\) nên \(\frac{{HD}}{{AD}} = \frac{{BM}}{{BG}}\).
Do đó \(\widehat {{M_1}} = \widehat {AHD}\), mà \(\widehat {AHD} = \widehat {BAH}\) (hai góc so le trong, \(AB//CD\))
Suy ra \(\widehat {{M_1}} = \widehat {BAH}\). Mà \(\widehat {{M_1}}\) và \(\widehat {BAH}\) ở vị trí đồng vị nên \(AH//MG\).