Áp dụng trường hợp đồng dạng thứ ba của tam giác vào tam giác vuông. Lời giải bài tập, câu hỏi Giải bài 48 trang 79 sách bài tập toán 8 – Cánh diều – Bài 8. Trường hợp đồng dạng thứ ba của tam giác. Cho hình bình hành \(ABCD\) \(\left( {AC > BD} \right)\). Từ \(C\) kẻ \(CE\) vuông góc với \(AB\) (\(E\…
Đề bài/câu hỏi:
Cho hình bình hành \(ABCD\) \(\left( {AC > BD} \right)\). Từ \(C\) kẻ \(CE\) vuông góc với \(AB\) (\(E\) thuộc đường thẳng \(AB\)), \(CF\) vuông góc với \(AD\) (\(F\) thuộc đường thẳng \(AD\)). Chứng minh: \(AB.AE + AD.AF = A{C^2}\).
Hướng dẫn:
Áp dụng trường hợp đồng dạng thứ ba của tam giác vào tam giác vuông:
Nếu tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Lời giải:
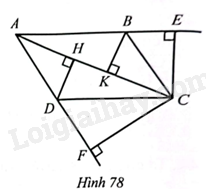
Gọi \(H,K\) lần lượt là hình chiếu của \(D,B\) trên đường thẳng \(AC\).
Ta có \(\Delta AHD\backsim \Delta AFC=>\frac{AD}{AC}=\frac{AH}{AF}\) hay \(AD.AF = AC.AH\) (1)
Tương tự \(\Delta AKB\backsim \Delta AEC=>\frac{AB}{AC}=\frac{AK}{AE}\) hay \(AB.AE = AC.AK\) (2).
Vì \(\Delta ABK\backsim \Delta CDH\) (cạnh huyền – góc nhọn) nên \(AK = HC\)
Từ đó, cộng (1) và (2) theo vế ta được:
\(AD.AF + AB.AE = AC.\left( {AH + AK} \right) = AC\left( {AH + HC} \right) = A{C^2}\).