Áp dụng trường hợp đồng dạng thứ ba: góc – góc Nếu hai góc của tam giác này lần lượt bằng hai góc của tam. Phân tích, đưa ra lời giải Giải bài 45 trang 78 sách bài tập toán 8 – Cánh diều – Bài 8. Trường hợp đồng dạng thứ ba của tam giác. Cho hình thang \(ABCD\) có \(AB//CD\), \(AB = 4\)cm, \(DB = 6\) cm và \(\widehat {DAB} = \widehat {DBC}\)….
Đề bài/câu hỏi:
Cho hình thang \(ABCD\) có \(AB//CD\), \(AB = 4\)cm, \(DB = 6\) cm và \(\widehat {DAB} = \widehat {DBC}\). Tính độ dài \(CD\).
Hướng dẫn:
Áp dụng trường hợp đồng dạng thứ ba: góc – góc
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
Lời giải:
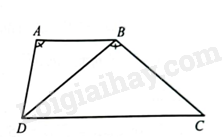
Ta có: \(\widehat {DAB} = \widehat {DBC}\) (giả thiết), \(\widehat {ABD} = \widehat {BDC}\) (hai góc so le trong). Suy ra \(\Delta ABD\backsim \Delta BDC\).
Do đó ta có \(\frac{{AB}}{{BD}} = \frac{{BD}}{{DC}}\), tức là \(CD = \frac{{B{D^2}}}{{AB}}\)
Từ đó: \(CD = \frac{{{6^2}}}{4} = 9\) (cm)