Bài 31 trang 32 SBT toán 8 – Cánh diều: Nhân dịp tết cổ truyền, lớp 8B tổ chức trò chơi “Vòng quay may mắn”

Đề bài/câu hỏi:

Nhân dịp tết cổ truyền, lớp 8B tổ chức trò chơi “Vòng quay may mắn”, trong đó chiếc đĩa hình trong được chia thành 11 phần bằng nhau và ghi các số 10,20,30,40,50,60,70,80,90,100,200; chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn 1 lần:

a) Viết tập hợp \(B\) gồm các kết quả có thể xảy ra đối với số ghi ở hình quạt mà chiếc kim chỉ vào khi đĩa dừng lại.

b) Tính xác suất của mỗi biến cố sau:

– “Chiếc kim chỉ vào hình quạt ghi số chia hết cho cả 5 và 14”;

– “Chiếc kim chỉ vào hình quạt ghi số có thể phân tích thành tổng của hai số khác nhau đã được ghi vào hình quạt, đồng thờ có một số lớn hơn 75”.

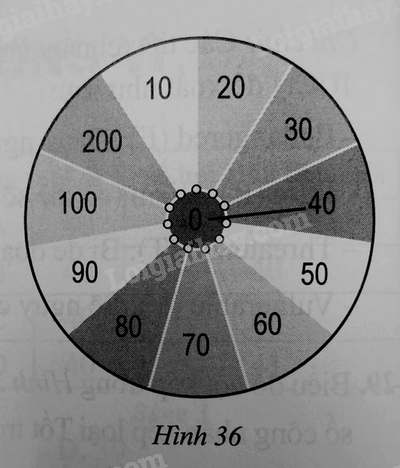
Hướng dẫn:

Một đĩa tròn bằng bìa cứng được chia làm \(n\) phần bằng nhau (\(n\) hình quạt bằng nhau) và ghi các số 1,2,3,4,…\(n\); chiếc kim được gắn cố định vào rục quay ở tâm của đĩa. Khi quay đĩa tròn đó một lần, chiếc kim sẽ chỉ vào một trong \(n\) hình quạt đó, nếu \(k\) là số kết quả thuận lợi cho một biến cố thì xác suất của biến cố đó bằng \(\frac{k}{n}\).

Lời giải:

a) \(B = \left\{ {10,20,30,40,50,60,70,80,90,100,200} \right\}\). Tập hợp \(B\) có 11 phần tử.

b) Có một kết quả thuận lợi cho biến cố “Chiếc kim chỉ vào hình quạt ghi số chia hết cho cả 5 và 14” là 70. Vì vậy, xác suất của biến cố đó là \(\frac{1}{{11}}\).

Có hai kết quả thuận lợi cho biến cố “Chiếc kim chỉ vào hình quạt, đồng thời một số lớn hơn 75” là: 90;100. Vì vậy, xác suất của biến cố đó là \(\frac{2}{{11}}\).