Dựa vào đồ thi của hàm số bậc nhất để tính tỉ số phần trăm giữa giá của thiết bị tiệt khuẩn đó sau 12. Hướng dẫn cách giải/trả lời Giải bài 26 trang 62 sách bài tập toán 8 – Cánh diều – Bài 4. Đồ thị của hàm số bậc nhất y = ax + b (a khác 0). Một thiết bị tiệt khuẩn y tế bằng năng lượng mặt trời được mua với giá 60 triệu đồng…
Đề bài/câu hỏi:
Một thiết bị tiệt khuẩn y tế bằng năng lượng mặt trời được mua với giá 60 triệu đồng, mỗi năm thiết bị tiệt khuẩn đó đều khấu hao \(k\) (triệu đồng) với \(0 < k < 60\). Gọi \(y\) (triệu đồng) là giá của thiết bị tiệt khuẩn đó sau \(x\) năm sử dụng.
a) Chứng tỏ rẳng \(y\) là hàm số bậc nhất của \(x\), tức là \(y = ax + b\left( {a \ne 0} \right)\).
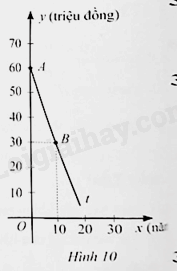
b) Trong Hình 10, tia \(At\) là một phần của đường thẳng \(y = ax + b\). Tìm \(a,b\). Từ đó, cho biết sau 12 năm sử dụng thì giá của thiết bị tiệt khuẩn đó bằng bao nhiêu phần trăm so với giá mua ban đầu.
Hướng dẫn:
Dựa vào đồ thi của hàm số bậc nhất để tính tỉ số phần trăm giữa giá của thiết bị tiệt khuẩn đó sau 12 năm sử dụng và giá mua ban đầu.
Lời giải:
a) Công thức biểu thị giá của thiết bị tiệt khuẩn đó sau \(x\) năm sử dụng là: \(y = 60 – kx\) hay \(y = – kx + 60\). Mà \(k \ne 0\), suy ra \(y\) là hàm số bậc nhất của \(x\).
b) Từ câu a, ta có \(b = 60\). Do đường thẳng \(y = ax + b\) đi qua điểm \(B\left( {10;30} \right)\) nên \(30 = a.10 + 60\). Suy ra \(a = – 3\). Khi đó, đường thẳng cần tìm là: \(y = – 3x + 60\).
Giá của thiết bị tiệt khuẩn đó sau 12 năm sử dụng là:
\( – 3.12 + 60 = 24\) (triệu đồng)
Tỉ số phần trăm giữa giá của thiết bị tiệt khuẩn đó sau 12 năm sử dụng và giá mua ban đầu là: \(\frac{{24.100}}{{60}}\% = 40\% \).
Vậy sau 12 năm sử dụng thì giá của thiết bị tiệt khuẩn đó bằng \(40\% \) so với giá mua ban đầu.