Dựa vào dấu hiệu nhận biết của hình bình hành. Trả lời Giải bài 16 trang 94 sách bài tập toán 8 – Cánh diều – Bài 4. Hình bình hành. Cho tam giác \(ABC\) có \(AB = AC = 3cm\). Từ điểm \(M\) thuộc cạnh \(BC\), kẻ \(MD\…
Đề bài/câu hỏi:
Cho tam giác \(ABC\) có \(AB = AC = 3cm\). Từ điểm \(M\) thuộc cạnh \(BC\), kẻ \(MD\) song song với \(AC\) và \(ME\) song song với \(AB\) (điểm \(D,E\) lần lượt thuộc cạnh \(AB,AC\)). Tính chu vi của tứ giác \(ADME\).
Hướng dẫn:
Dựa vào dấu hiệu nhận biết của hình bình hành:
– Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành
– Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành
– Tứ giác có hai cặp góc đối bằng nhau là hình bình hành
– Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
Lời giải:
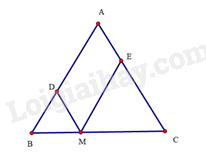
Do \(AB = AC\) nên tam giác \(ABC\) cân tại \(A\). Suy ra \(\widehat {ABC} = \widehat {ACB}\).
Mà \(\widehat {ABC} = \widehat {EMC}\) (hai góc đồng vị), suy ra \(\widehat {ACB} = \widehat {EMC}\).
Do đó, tam giác \(ECM\) cân tại \(E\). Suy ra \(ME = CE\).
Tứ giác \(ADME\) có \(MD//AE,ME//AD\) nên \(ADME\) là hình bình hành. Vậy chu vi của hình bình hành \(ADME\) là:
\(2\left( {AE + ME} \right) = 2\left( {AE + CE} \right) = 2AC = 6cm\)