Chứng minh tam giác BAD và ABC bằng nhau. Lời giải Giải bài 4 trang 71 vở thực hành Toán 7 – Bài 15. Các trường hợp bằng nhau của tam giác vuôn. Bài 4. Cho hình vẽ bên. Biết \(\widehat {DAC} = \widehat {CBD} = {90^o},AD = BC\),…
Đề bài/câu hỏi:
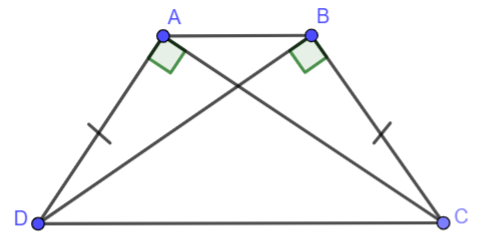
Bài 4. Cho hình vẽ bên. Biết \(\widehat {DAC} = \widehat {CBD} = {90^o},AD = BC\), hãy chứng minh rằng \(\widehat {BAD} = \widehat {ABC}\).
Hướng dẫn:
Chứng minh tam giác BAD và ABC bằng nhau.
Lời giải:
Ta thấy hai tam giác ADC và BCD lần lượt vuông góc tại các đỉnh A, B và có:
DC là cạnh chung
AD = BC (theo giả thiết)
Vậy \(\Delta ADC = \Delta BCD\)(cạnh huyền – cạnh góc vuông). Từ đây suy ra AC = BD.
Hai tam giác BAD và ABC có: AD = BC (theo giả thiết), AB là cạnh chung, BD = AC (theo chứng minh trên). Vậy \(\Delta BAD = \Delta ABC\)(hai cạnh góc vuông).
Suy ra \(\widehat {BAD} = \widehat {ABC}\).