Chứng minh hai tam giác AHC và A’H’C’ bằng nhau. Hướng dẫn giải Giải bài 5 trang 71 vở thực hành Toán 7 – Bài 15. Các trường hợp bằng nhau của tam giác vuôn. Bài 5. Cho hình vẽ dưới đây. Biết AB =A’B’, HB = H’B’, BC = B’C’….
Đề bài/câu hỏi:
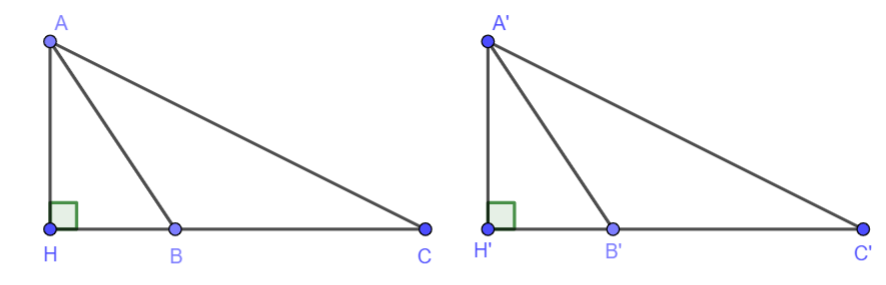
Bài 5. Cho hình vẽ dưới đây. Biết AB =A’B’, HB = H’B’, BC = B’C’.
Chứng minh rằng AC = A’C’.
Hướng dẫn:
Chứng minh hai tam giác AHC và A’H’C’ bằng nhau.
Lời giải:
Hai tam giác AHB và A’H’B’ lần lượt vuông tại đỉnh H, H’ và có:
AB = A’B’, HB = H’B’ (theo giả thiết)
Vậy \(\Delta AHB = \Delta A’H’B’\)(hai cạnh góc vuông). Do đó AH = A’H’.
Hai tam giác AHC và A’H’C’ lần lượt vuông tại đỉnh H, H’ và có:
AH = A’H’ (theo chứng minh trên)
HC = HB + BC = H’B’ + B’C’ = H’C’ (theo giả thiết)
Vậy \(\Delta AHC = \Delta A’H’C’\)(hai cạnh góc vuông). Do đó AC = A’C’.