Ta sẽ xem mắt phẳng nước biển là độ cao 0, rồi sẽ dựa vào các điểm ở vị trí để biết độ cao so. Giải và trình bày phương pháp giải Giải bài 1 trang 22 vở thực hành Toán 7 – Bài tập cuối chương 1. Hình 1.4 mô phỏng vị trí của năm điểm A, B, C, D, E so với mực nước biển….
Đề bài/câu hỏi:
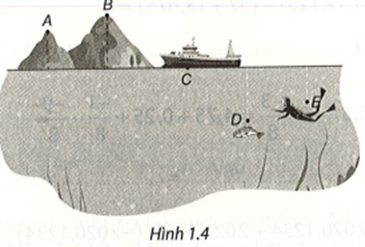
Hình 1.4 mô phỏng vị trí của năm điểm A, B, C, D, E so với mực nước biển. Biết rằng độ cao (tính theo đơn vị kilômét) so với mực nước biển của mỗi điểm là 1 trong các số sau:
\(\frac{{33}}{{12}};\frac{{79}}{{30}}; – \frac{{25}}{{12}}; – \frac{5}{6};0.\)
Hướng dẫn:
– Ta sẽ xem mắt phẳng nước biển là độ cao 0, rồi sẽ dựa vào các điểm ở vị trí để biết độ cao so với mực nước biển.
– So sánh bằng cách quy đồng mẫu số của chúng về 60 rồi so sánh tử số.
Lời giải:
Ta có:
\(\frac{{33}}{{12}} = \frac{{33.5}}{{60}} = \frac{{165}}{{60}};\)
\(\frac{{79}}{{30}} = \frac{{79.2}}{{60}} = \frac{{158}}{{60}};\)
\( – \frac{{25}}{{12}} = – \frac{{25.5}}{{12.5}} = \frac{{ – 125}}{{60}};\)
\(\frac{{ – 5}}{6} = \frac{{ – 5.10}}{{6.10}} = \frac{{ – 50}}{{60}}\)
Nên ta có:
\(\frac{{ – 125}}{{60}} < \frac{{ – 50}}{{60}} < 0 < \frac{{158}}{{60}} < \frac{{165}}{{60}}\)
Căn cứ mô phỏng các vị trí điểm A, B, C, D, E ta được:
\(A\left( {\frac{{79}}{{30}}} \right),B\left( {\frac{{33}}{{12}}} \right),C\left( 0 \right),D\left( {\frac{{ – 25}}{{12}}} \right),E\left( {\frac{{ – 5}}{6}} \right)\)