Hướng dẫn giải Hoạt động 3 Bài 3. Tam giác cân (trang 60, 61, 62) – SGK Toán 7 Chân trời sáng tạo. Gợi ý: Ta chứng minh \(\Delta AHB = \Delta CHB\) rồi từ đó suy ra BA = BC.
Câu hỏi/Đề bài:
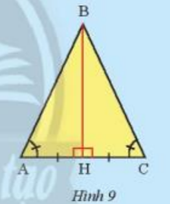
Cho tam giác ABC có \(\widehat A\)=\(\widehat C\). Vẽ đường thẳng đi qua điểm B, vuông góc với AC và cắt AC tại điểm H (Hình 9). Em hãy làm theo gợi ý sau để chứng minh BA = BC.
Xét \(\Delta AHB\)và \(\Delta CHB\)cùng vuông tại H, ta có:
BH là cạnh góc vuông ?
\(\widehat {HAB}\) = \(\widehat {HCB}\) suy ra \(\widehat {ABH} = \widehat {CBH}\) (?)
Vậy \(\Delta AHB = \Delta CHB\). Suy ra BA = BC
Hướng dẫn:
Ta chứng minh \(\Delta AHB = \Delta CHB\) rồi từ đó suy ra BA = BC
Lời giải:
Xét \(\Delta AHB\) và \(\Delta CHB\) cùng vuông tại H, ta có:
BH là cạnh góc vuông của và
\(\widehat {ABH} = \widehat {CBH}\)( Do cùng bằng \({90^o} – \widehat {HAB} = {90^o} – \widehat {HCB}\) )
\( \Rightarrow \) \(\Delta AHB = \Delta CHB\)
\( \Rightarrow \) BA = BC