Chứng minh 2 tam giác bằng nhau (c-c-c) Chứng minh 2 góc ở vị trí so le trong bằng nhau. Giải chi tiết Giải bài 6 trang 58 SGK Toán 7 tập 2 – Chân trời sáng tạo – Bài 2. Tam giác bằng nhau. Cho Hình 25 có EF = HG, EG = HF. Chứng minh rằng:…
Đề bài/câu hỏi:
Cho Hình 25 có EF = HG, EG = HF. Chứng minh rằng:
a) \(\Delta EFH=\Delta HGE\)
b) EF // HG
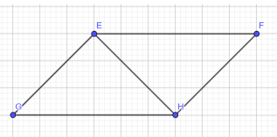
Hướng dẫn:
– Chứng minh 2 tam giác bằng nhau (c-c-c)
– Chứng minh 2 góc ở vị trí so le trong bằng nhau
Lời giải:
a) Xét \(\Delta EFH\) và \(\Delta HGE\) có :
EF = HG; FH = GE; EH chung
\(\Rightarrow \Delta EFH=\Delta HGE\) (c-c-c)
\( \Rightarrow \widehat {FEH} = \widehat {EHG}\)( 2 góc tương ứng )
b) Vì \(\widehat {FEH}=\widehat {EHG}\)
Mà 2 góc này ở vị trí so le trong
Do đó, EF // HG (Dấu hiệu nhận biết)