Ta chứng minh AT = RT bằng cách chứng minh tam giác ATR cân tại T Để chứng minh tam giác ART cân tại T. Gợi ý giải Giải bài 5 trang 82 SGK Toán 7 tập 2 – Chân trời sáng tạo – Bài 9. Tính chất ba đường phân giác của tam giác. Cho tam giác AMN vuông tại A. Tia phân giác của góc M và N cắt nhau tại I….
Đề bài/câu hỏi:
Cho tam giác AMN vuông tại A. Tia phân giác của góc M và N cắt nhau tại I. Tia MI cắt AN tại R. Kẻ RT vuông góc với AI tại T. Chứng minh rằng AT = RT.
Hướng dẫn:
– Ta chứng minh AT = RT bằng cách chứng minh tam giác ATR cân tại T
– Để chứng minh tam giác ART cân tại T ta sử dụng tính chất 2 góc đáy trong tam giác bằng nhau
Lời giải:
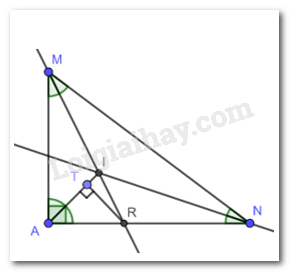
Theo đề bài ta có tia phân giác của góc M, N cắt nhau tại I
\( \Rightarrow \) I là điểm giao của 3 phân giác trong tam giác AMN
\( \Rightarrow \) AI là phân giác của góc A
\( \Rightarrow \) \(\widehat {IAN} = \widehat {IAM} = {45^o}\)(góc A vuông)
Xét tam giác ATR có \(\widehat {IAN} = {45^o}\) và \(\widehat {ATR} = {90^o}\) theo định lí tổng 3 góc trong 1 tam giác
\( \Rightarrow \widehat {IAN} + \widehat {ATR} + \widehat {TRA} = {180^o} \Rightarrow \widehat {TRA} = {180^o} – {90^o} – {45^o} = {45^o}\)
\( \Rightarrow \Delta ATR \) vuông cân tại T ( tam giác có 2 góc ở đáy = 45 độ )
\( \Rightarrow AT = TR\)