Ta chứng minh 2 tam giác ABD và ACD bằng nhau Suy ra 2 tam giác BAM và CAM bằng nhau \( \Rightarrow \. Trả lời Giải bài 4 trang 70 SGK Toán 7 tập 2 – Chân trời sáng tạo – Bài 5. Đường trung trực của một đoạn thẳng. Quan sát Hình 13, biết AB = AC, DB = DC. Chứng minh rằng M là trung điểm của BC….
Đề bài/câu hỏi:
Quan sát Hình 13, biết AB = AC, DB = DC. Chứng minh rằng M là trung điểm của BC.
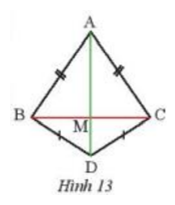
Hướng dẫn:
– Ta chứng minh 2 tam giác ABD và ACD bằng nhau
– Suy ra 2 tam giác BAM và CAM bằng nhau \( \Rightarrow \) BM = CM
Lời giải:
Xét tam giác ABD và tam giác ACD có :
AB = AC ( giả thiết )
BD = CD ( giả thiết )
AD cạnh chung
\( \Rightarrow \Delta ABD =\Delta ACD (c-c-c)\)
\( \Rightarrow \)\(\widehat {BAD} = \widehat {CAD}\)( 2 góc tương ứng )
Xét tam giác ABM và ta giác ACM có :
AB = AC ( giả thiết )
AM cạnh chung
\(\widehat {BAD} = \widehat {CAD}\)( chứng minh trên )
\(\Delta ABM=\Delta ACM (c-g-c)\)
\(\Rightarrow MC = MB\) ( 2 cạnh tương ứng )
\( \Rightarrow \) M là trung điểm BC