Ta chứng minh I là giao của 3 đường phân giác trong tam giác ABC Từ đó ta chứng minh CI là phân giác góc. Lời giải bài tập, câu hỏi Giải bài 2 trang 82 SGK Toán 7 tập 2 – Chân trời sáng tạo – Bài 9. Tính chất ba đường phân giác của tam giác. Cho tam giác ABC cân tại A. Kẻ đường trung tuyến AM….
Đề bài/câu hỏi:
Cho tam giác ABC cân tại A. Kẻ đường trung tuyến AM. Tia phân giác của góc B cắt AM tại I. Chứng minh rằng CI là tia phân giác của góc C.
Hướng dẫn:
– Ta chứng minh I là giao của 3 đường phân giác trong tam giác ABC
– Từ đó ta chứng minh CI là phân giác góc C
Lời giải:
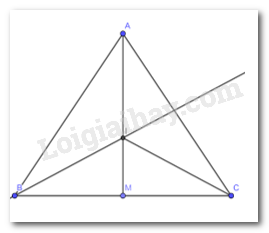
Xét tam giác ABM và tam giác ACM có :
AM chung
BM = CM ( M là trung điểm BC )
AB = AC (tam giác ABC cân tại A theo giả thiết)
\( \Rightarrow \Delta AMB = \Delta AMC (c-c-c)\)
\( \Rightarrow \widehat{BAM}= \widehat{CAM}\) (2 góc tương ứng)
\( \Rightarrow \) AM thuộc tia phân giác của góc A
Mà AM cắt tia phân giác góc B tại I
\( \Rightarrow \) I là giao của các đường phân giác trong tam giác ABC
\( \Rightarrow \) CI là phân giác góc C (định lí 3 đường phân giác cắt nhau tại 1 điểm)