Sử dụng định lí tổng 3 góc trong tam giác. Trả lời Giải bài 2 trang 47 SGK Toán 7 tập 2 – Chân trời sáng tạo – Bài 1. Góc và cạnh của một tam giác. Tính số đo x của góc trong Hình 6….
Đề bài/câu hỏi:
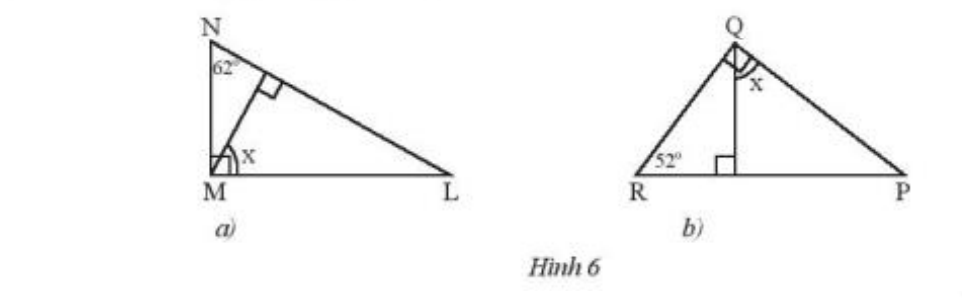
Tính số đo x của góc trong Hình 6.
Hướng dẫn:
Sử dụng định lí tổng 3 góc trong tam giác.
Lời giải:
a) Cách 1: Gọi MP vuông góc với NL (P thuộc NL)
Xét tam giác MNL vuông tại M ta có:
\( \Rightarrow \widehat L = {90^o} – \widehat N =90^0-62^0={28^o}\)
Xét tam giác MPL vuông tại P ta có:
\( \Rightarrow \widehat x = {90^o} – \widehat L = {90^o} – {28^o} = {62^o}\)
Cách 2:
Xét tam giác MNP vuông tại P ta có:
\( \Rightarrow \widehat{NMP} +\widehat N =90^0\)
Mà \(\widehat{NMP} +x =90^0\)
\( \Rightarrow \widehat N =x \Rightarrow x=62^0\)
b) Cách 1: Gọi QF vuông góc với RP (F thuộc RP)
Xét tam giác RQP vuông tại Q ta có:
\( \Rightarrow \widehat R + \widehat P = {90^o} \Rightarrow \widehat P = {90^o} – {52^o} = {38^o}\)
Xét tam giác QFP vuông tại F ta có: \( \Rightarrow \widehat x + \widehat P = {90^o} \Rightarrow \widehat x = {90^o} – {38^o} = {52^o}\)
Cách 2:
Xét tam giác QRF vuông tại F ta có:
\( \Rightarrow \widehat{RQF} +\widehat R =90^0\)
Mà \(\widehat{RQF} +x =90^0\)
\( \Rightarrow \widehat R =x \Rightarrow x=52^0\)