Tổng ba góc trong một tam giác bằng 180°. b) Chứng minh \(\Delta ABD = \Delta AED\) theo trường hợp g. c. Hướng dẫn giải Giải bài 5 trang 92 SGK Toán 7 tập 2 – Cánh diều – Bài 6. Trường hợp bằng nhau thứ ba của tam giác: góc- cạnh – góc. Cho tam giác ABC có…
Đề bài/câu hỏi:
Cho tam giác ABC có \(\widehat B > \widehat C\). Tia phân giác góc BAC cắt cạnh BC tại điểm D.
a) Chứng minh \(\widehat {ADB} < \widehat {ADC}\).
b) Kẻ tia Dx nằm trong góc ADC sao cho \(\widehat {ADx} = \widehat {ADB}\). Giả sử tia Dx cắt cạnh AC tại điểm E. Chứng minh: \(\Delta ABD = \Delta AED,AB < AC\).
Hướng dẫn:
a) Tổng ba góc trong một tam giác bằng 180°.
b) Chứng minh \(\Delta ABD = \Delta AED\) theo trường hợp g.c.g và AB < AC vì cạnh đối diện với góc lớn hơn thì lớn hơn.
Lời giải:
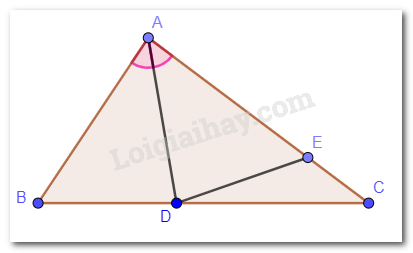
a) Ta có: \(\widehat {BAD} = \widehat {CAD}\)(vì AD là phân giác của góc BAC).
Mà \(\widehat B > \widehat C\)nên \(\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\).
Tổng ba góc trong một tam giác bằng 180° nên:
\(\begin{array}{l}\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\\ \to 180^\circ – (\widehat B + \widehat {BAD}) < 180^\circ – (\widehat C + \widehat {CAD})\\ \to \widehat {ADB} < \widehat {ADC}\end{array}\)
b) Xét hai tam giác ADB và tam giác ADE có:
\(\widehat {ADB} = \widehat {ADE}\);
AD chung;
\(\widehat {BAD} = \widehat {EAD}\).
Vậy \(\Delta ABD = \Delta AED\) (g.c.g)
Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn.
Trong tam giác ABC có \(\widehat B > \widehat C\) nên AC > AB hay AB < AC (AB là cạnh đối diện với góc C, AC là cạnh đối diện với góc B).