Dựa vào tính chất của đường trung trực: Một điểm thuộc đường trung trực thì cách đều hai đầu mút. Vận dụng kiến thức giải Giải bài 4 trang 103 SGK Toán 7 tập 2 – Cánh diều – Bài 9. Đường trung trực của một đoạn thẳng. Cho đường thẳng d là đường trung trực của đoạn thẳng AB….
Đề bài/câu hỏi:
Cho đường thẳng d là đường trung trực của đoạn thẳng AB. Điểm M không thuộc đường thẳng d và đoạn thẳng AB sao cho đường thẳng d cắt đoạn thẳng MB tại điểm I. Chứng minh:
a) \(MB = AI + IM\);
b) MA < MB.
Hướng dẫn:
a) Dựa vào tính chất của đường trung trực: Một điểm thuộc đường trung trực thì cách đều hai đầu mút.
b) Dựa vào tính chất trong tam giác: Tổng hai cạnh bất kì luôn lớn hơn độ dài cạnh còn lại.
Lời giải:
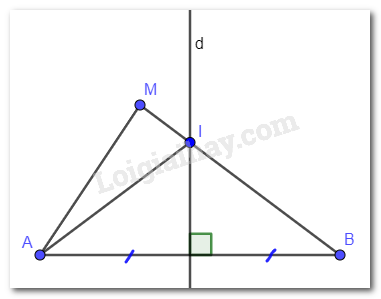
a) Ta có: Đường thẳng d là đường trung trực của đoạn thẳng AB. Mà điểm I thuộc đường thẳng d nên suy ra: IA = IB. (Một điểm thuộc đường trung trực thì cách đều hai đầu mút).
Ta có: \(MB = MI + IB\) mà IA = IB nên \(MB = MI + IA = AI + IM\).
b) Xét tam giác AMI có: \(MA < AI + IM\)(Tổng hai cạnh bất kì trong một tam giác luôn lớn hơn độ dài cạnh còn lại) mà \(MB = AI + IM\).
Vậy \(MA < MB\).