Chứng minh BM = CN bằng cách chứng minh tam giác ABM bằng tam giác ACN. b) Chứng minh \(\Delta GBC\. Lời giải bài tập, câu hỏi Giải bài 2 trang 107 SGK Toán 7 tập 2 – Cánh diều – Bài 10. Tính chất ba đường trung tuyến của tam giác. Cho tam giác ABC cân tại A, hai đường trung tuyến BM và CN cắt nhau tại G. Chứng minh:…
Đề bài/câu hỏi:
Cho tam giác ABC cân tại A, hai đường trung tuyến BM và CN cắt nhau tại G. Chứng minh:
a) BM = CN; b) \(\Delta GBC\) cân tại G.
Hướng dẫn:
a) Chứng minh BM = CN bằng cách chứng minh tam giác ABM bằng tam giác ACN.
b) Chứng minh \(\Delta GBC\) cân tại G bằng cách chứng minh GB = GC.
Lời giải:
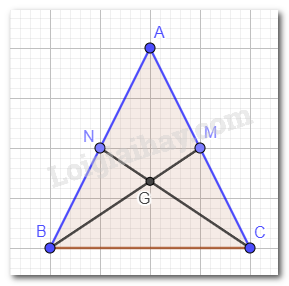
a) Tam giác ABC cân tại A nên AB = AC. M, N lần lượt là trung điểm của cạnh AC, AB nên AM = AN.
Xét tam giác ABM và tam giác ACN có: AM = AN; \(\widehat A\)chung; AB = AC.
Vậy \(\Delta ABM = \Delta ACN\)(c.g.c) hay BM = CN.
b) Xét tam giác ABC có G là giao điểm của hai đường trung tuyến BM và CN nên G là trọng tâm tam giác ABC. Do đó:
\(GB = \dfrac{2}{3}BM;GC = \dfrac{2}{3}CN\). Mà BM = CN nên GB = GC.
Vậy tam giác GBC cân tại G.