Kẻ \(MH \bot d, M’H’ \bot d\) -Chứng minh: \(\Delta MHH’\)=\(\Delta H’M’M\. Trả lời Giải Bài 9.6 trang 50 sách bài tập toán 7 – Kết nối tri thức với cuộc sống – Bài 32. Quan hệ giữa đường vuông góc và đường xiên. Cho 2 điểm phân biệt M, M’ ở cùng phía đối với đường thẳng d (M, M’ không thuộc d)….
Đề bài/câu hỏi:
Cho 2 điểm phân biệt M, M’ ở cùng phía đối với đường thẳng d (M, M’ không thuộc d). Chứng minh rằng nếu M, M’ có cùng khoảng cách đến đường thẳng d thì MM’ song song với d.
Hướng dẫn:
-Kẻ \(MH \bot d,M’H’ \bot d\)
-Chứng minh: \(\Delta MHH’\)=\(\Delta H’M’M\)
Lời giải:
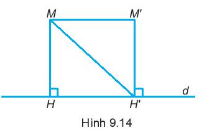
Kẻ \(MH \bot d,M’H’ \bot d\)
\( \Rightarrow MH\parallel M’H’\)
Xét \(\Delta MHH’\) và \(\Delta H’M’M\) có:
MH’ chung
MH = H’M’ (gt)
\(\begin{array}{l}\widehat {HMH’} = \widehat {M’H’M}\left( {so\,le\,trong} \right)\\ \Rightarrow \Delta MHH’ = \Delta H’M’M\left( {g – c – g} \right)\\ \Rightarrow \widehat {MH’H} = \widehat {H’MM’}\end{array}\)
Mà 2 góc ở vị trí so le trong nên \(MM’\parallel d\) (Dấu hiệu nhận biết 2 đường thẳng song song).