Chỉ ra các cạnh tương ứng bằng nhau. b) -Chứng minh \(\widehat {DAB} = \widehat {ADC}\) -Chứng minh \(\widehat {ADC} = {90^0}\). Vận dụng kiến thức giải Giải bài 4.20 trang 58 sách bài tập toán 7 – Kết nối tri thức với cuộc sống – Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác. Cho hình bình hành ABCD có hai đường chéo AC và BD bằng nhau (H.4….
Đề bài/câu hỏi:
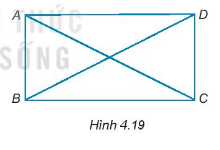
Cho hình bình hành ABCD có hai đường chéo AC và BD bằng nhau (H.4.19)
a) Chứng minh \(\Delta ABD = \Delta DCA;\Delta ADC = \Delta BCD\).
b) Bằng cách tính số đo góc ADC, hãy cho biết ABCD có phải là hình chữ nhật không.
Hướng dẫn:
a) Chỉ ra các cạnh tương ứng bằng nhau.
b)
-Chứng minh \(\widehat {DAB} = \widehat {ADC}\)
-Chứng minh \(\widehat {ADC} = {90^0}\).
Lời giải:
a)
Xét \(\Delta ABD\)và \(\Delta DCA\)có:
AB = DC (2 cạnh đối của hình bình hành)
BD = CA (gt)
AD: Cạnh chung
\( \Rightarrow \Delta ABD = \Delta DCA\left( {c – c – c} \right)\)
Xét \(\Delta ADC\) và \(\Delta BCD\) có:
AD = BC (2 cạnh đối của hình bình hành)
AC = BD (gt)
DC: Cạnh chung
\( \Rightarrow \Delta ADC = \Delta BCD\left( {c – c – c} \right)\)
b)
Ta có: \(\Delta ABD = \Delta BCD\left( {cmt} \right) \Rightarrow \widehat {DAB} = \widehat {ADC}\) (góc tương ứng).
Mặt khác vì ABCD là hình bình hành nên \(\widehat {DAB} + \widehat {ADC} = {180^0} \Rightarrow \widehat {DAB} = \widehat {ADC} = \dfrac{{{{180}^0}}}{2} = {90^0}\)
Hình bình hành ABCD có một góc vuông nên là hình chữ nhật.