Chứng minh: \(\Delta AMH = \Delta AMK\)suy ra: MH = MK Chứng minh: \(\widehat B = \widehat C\. Giải và trình bày phương pháp giải Giải Bài 2 trang 60 sách bài tập toán 7 – Chân trời sáng tạo – Bài 7: Tính chất ba đường trung tuyến của tam giác. Cho tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác của góc A….
Đề bài/câu hỏi:
Cho tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác của góc A. Chứng minh tam giác ABC là tam giác cân.
Hướng dẫn:
– Chứng minh: \(\Delta AMH = \Delta AMK\)suy ra: MH = MK
– Chứng minh: \(\widehat B = \widehat C\) suy ra tam giác ABC cân
Lời giải:
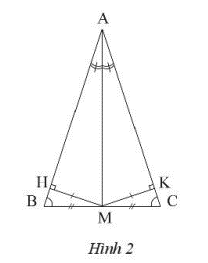
Vẽ đường cao MH của tam giác AMB và vẽ đường cao MK của tam giác AMC.
Ta có \(\Delta AMH = \Delta AMK\)(vì hai tam giác vuông có chung cạnh huyền AM, và một góc nhọn bằng nhau)
Suy ra: MH = MK.
Từ đó, ta có: \(\Delta MBH = \Delta MCK\) (hai tam giác vuông có chung cạnh huyền Am và một cạnh góc vuông bằng nhau: MH = MK)
Suy ra \(\widehat B = \widehat C\)
Vậy tam giác ABC là tam giác cân tại A.