So sánh đường cao và các cạnh đáy tương ứng của các tam giác. Phân tích, đưa ra lời giải Giải Bài 1 trang 60 sách bài tập toán 7 – Chân trời sáng tạo – Bài 7: Tính chất ba đường trung tuyến của tam giác. Cho tam giác ABC có trung tuyến AM và G là trọng tâm….
Đề bài/câu hỏi:
Cho tam giác ABC có trung tuyến AM và G là trọng tâm. Chứng minh:
|
a) \({S_{AMB}} = {S_{AMC}}\) |
b) \({S_{ABG}} = 2{S_{BMG}}\) |
c) \({S_{GAB}} = {S_{GBC}} = {S_{GAC}}\) |
Hướng dẫn:
So sánh đường cao và các cạnh đáy tương ứng của các tam giác
Lời giải:
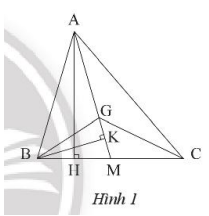
a) Vẽ đường cao AH của tam giác ABC.
Hai tam giác AMB và AMC có cùng đường cao AH và có cạnh đáy bằng nhau: BM = CM
Suy ra: \({S_{AMB}} = {S_{AMC}}\)(vì \({S_{AMB}} = \frac{1}{2}.AH.BM{;^{}}{S_{AMC}} = \frac{1}{2}.AN.CM\))
b) Vẽ đường cao BK của tam giác BGM.
Hai tam giác ABG và BMG có cùng đường cao BK và có cạnh đáy AG = 2MG.
Suy ra: \({S_{ABG}} = \frac{1}{2}.BK.AG = \frac{1}{2}.BK.2MG = 2.\frac{1}{2}.BK.MG = 2{S_{BMG}}\)
c) Ta có:
\({S_{ABG}} = \frac{2}{3}{S_{ABM}} = \frac{1}{3}{S_{ABC}}\)
Tương tự: \({S_{ACG}} = \frac{2}{3}{S_{ACM}} = \frac{1}{3}{S_{ABC}}\)
Suy ra: \({S_{BCG}} = \frac{1}{3}{S_{ABC}}\)
Vậy: \({S_{GAB}} = {S_{GBC}} = {S_{GAC}} = \frac{1}{3}{S_{ABC}}\)