Giải chi tiết Lời giải Đề thi học kì 1 – Đề số 7 – Đề thi đề kiểm tra Toán lớp 7 Kết nối tri thức.
Câu hỏi/Đề bài:
Phần I: Trắc nghiệm:
|
1.A |
2.A |
3.B |
4.D |
5.D |
6.A |
7.B |
8.D |
9. A |
10.B |
Câu 1
Hướng dẫn:
Số đối của số hữu tỉ \(a\) kí hiệu là \( – a\).
Cách giải:
Số đối của \(\dfrac{{ – 7}}{{12}}\) là: \( – \left( {\dfrac{{ – 7}}{{12}}} \right) = \dfrac{7}{{12}}\)
Chọn A.
Câu 2
Hướng dẫn:
Sử dụng phương pháp so sánh trung gian.
Cách giải:
+ Ta có: \(37 < 41\) nên \(\dfrac{{37}}{{41}} – 1\) (1)
\(23 > 17\) nên \(\dfrac{{23}}{{17}} > 1\) suy ra \(\dfrac{{23}}{{ – 17}} < – 1\) (2)
Từ (1) và (2), suy ra \(\dfrac{{23}}{{ – 17}} < – 1 \dfrac{{23}}{{ – 17}}\)
Vậy đáp án A đúng.
Chọn A.
Câu 3
Hướng dẫn:
Căn bậc hai số học của số \(a\) không âm là số \(x\) không âm sao cho \({x^2} = a\).
Sử dụng tính chất: \({x^2} = {\left( { – x} \right)^2}\)
Cách giải:
\(\sqrt {{{\left( { – \dfrac{2}{3}} \right)}^2}} = \sqrt {{{\left( {\dfrac{2}{3}} \right)}^2}} = \sqrt {\dfrac{4}{9}} = \dfrac{2}{3}\) nên đáp án A,C,D đúng
Do chỉ tồn tại căn bậc hai số học của một số không âm nên đáp án B sai.
Chọn B.
Câu 4
Hướng dẫn:
Vận dụng kiến thức giá trị tuyệt đối của một số thực, tìm phát biểu sai.
Cách giải:
Phát biểu A đúng vì giá trị tuyệt đối của một số thực là một số không âm.
Phát biểu B đúng vì hai số có giá trị tuyệt đối bằng nhau là hai số bằng nhau hoặc đối nhau.
Phát biểu C đúng vì hai số đối nhau có điểm biểu diễn cách đều điểm gốc 0 nên giá trị tuyệt đối của chúng bằng nhau.
Phát biểu D sai vì giá trị tuyệt đối của số âm là số đối của nó.
Chọn D.
Câu 5
Hướng dẫn:
Hai góc kề bù có tổng số đo bằng \({180^0}\)
Hai đường thẳng song song thì hai góc ở vị trí đồng vị bằng nhau.
Vận dụng định lý: Tổng ba góc trong một tam giác bằng \({180^0}\).
Cách giải:
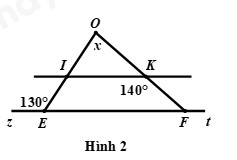
* Ta có: \(\angle zEO + \angle OEF = {180^0}\) (hai góc kề bù)
\(\begin{array}{l} \Rightarrow {130^0} + \angle OEF = {180^0}\\ \Rightarrow \angle OEF = {180^0} – {130^0}\\ \Rightarrow \angle OEF = {50^0}\end{array}\)
* \(IK//EF\) (giá thiết) \( \Rightarrow \angle OEF = \angle OIK\) (hai góc đồng vị) do đó, \(\angle OIK = {50^0}\)
* Ta có: \(\angle IKO + \angle IKF = {180^0}\) (hai góc kề bù)
\(\begin{array}{l} \Rightarrow \angle IKO + {140^0} = {180^0}\\ \Rightarrow \angle IKO = {180^0} – {140^0}\\ \Rightarrow \angle IKO = {40^0}\end{array}\)
* Xét \(\Delta OIK\) có: \(\angle O + \angle OIK + \angle OKI = {180^0}\) (định lí tổng ba góc trong một tam giác)
\(\begin{array}{l} \Rightarrow x + {50^0} + {40^0} = {180^0}\\ \Rightarrow x + {90^0} = {180^0}\\ \Rightarrow x = {180^0} – {90^0}\\ \Rightarrow x = {90^0}\end{array}\)
Vậy \(x = {90^0}\)
Chọn D.
Câu 6
Hướng dẫn:
+ Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
+ Hai tam giác bằng nhau có các cặp cạnh, cặp góc tương ứng bằng nhau
Cách giải:
Vì \(AK\) là tia phân giác của \(\angle BAC\) nên \(\angle {A_1} = \angle {A_2}\)
Theo giả thiết ta có: \(BH \bot AK \Rightarrow \angle AHB = \angle AHD = 90^\circ \)
Xét tam giác \(AHB\) và tam giác \(AHD\) có:
\(\angle {A_1} = \angle {A_2}\)
\(AH\) là cạnh chung
\(\angle AHB = \angle AHD = 90^\circ \)
Nên \(\Delta AHB = \Delta AHD\) (g.c.g)
Suy ra: \(HB = HD\) (hai cạnh tương ứng) nên B đúng
\(AB = AD\) (hai cạnh tương ứng) nên C đúng
\(\angle ABH = \angle ADH\) (hai góc tương ứng) nên D đúng
Chọn A.
Câu 7
Hướng dẫn:
Đọc và phân tích dữ liệu của biểu đồ hình quạt tròn.
Cách giải:
Số phần trăm học sinh đăng ký môn Toán là: \(100\% – 32,5\% – 30\% = 37,5\% \)
Chọn B.
Câu 8
Hướng dẫn:
Sử dụng biểu đồ cột kép, quan sát và trả lời câu hỏi.
Cách giải:
*) Chiều cao trung bình của nam:
Việt Nam: \(162,1cm\)
Singapore: \(171cm\)
Nhật Bản: \(172cm\)
Hàn Quốc: \(170,7cm\)
*) Chiều cao trung bình của nữ:
Việt Nam: \(152,2cm\)
Singapore:\(160cm\)
Nhật Bản: \(158cm\)
Hàn Quốc: \(157,4cm\)
Sự chênh lệch chiều cao giữa nam và nữ ở Việt Nam là:
\(162,1 – 152,2 = 9,9\,\,\left( {cm} \right)\)
Sự chênh lệch chiều cao giữa nam và nữ ở Singapore là:
\(171 – 160 = 11\,\,\left( {cm} \right)\)
Sự chênh lệch chiều cao giữa nam và nữ ở Nhật Bản là:
\(172 – 158 = 4\,\,\left( {cm} \right)\)
Sự chênh lệch chiều cao giữa nam và nữ ở Hàn Quốc là:
\(170,7 – 157,4 = 13,3\,\,\left( {cm} \right)\)
Sự chênh lệch chiều cao giữa nam và nữ ở Hàn Quốc là lớn nhất.
Chọn D.
Câu 9
Hướng dẫn:
Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
Cách giải:
Phát biểu định lí: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Chọn A.
Câu 10
Hướng dẫn:
\(Oz\) là tia phân giác của \(\angle xOy\) thì ta có: \(\angle xOz = \angle zOy = \dfrac{{\angle xOy}}{2}\)
\(\angle xOz\) và \(\angle zOy\) là hai góc kề nhau thì ta có: \(\angle xOz + \angle zOy = \angle xOy\).
\(\angle xOz\) và \(\angle zOy\) là hai góc kề bù thì ta có: \(\angle xOy = \angle xOz + \angle zOy = {180^0}\)
Cách giải:
Vì \(Om\) là tia phân giác của \(\angle xOy\) nên \(\angle mOy = \dfrac{{\angle xOy}}{2} = \dfrac{{{{50}^0}}}{2} = {25^0}\)
Ta có: \(\angle nOy\) và \(\angle yOx\) là hai góc kề bù nên \(\angle nOy + \angle yOx = {180^0}\)
\(\begin{array}{l} \Rightarrow \angle nOy + {50^0} = {180^0}\\ \Rightarrow \angle nOy = {180^0} – {50^0} = {130^0}\end{array}\)
Ta có: \(\angle nOy\) và \(\angle yOm\) là hai góc kề nhau nên \(\angle nOy + \angle yOm = \angle nOm\)
\( \Rightarrow {130^0} + {25^0} = {155^0} = \angle nOm\)
Vậy \(\angle mOn = {155^0}\)
Chọn B.
Phần II. Tự luận (7 điểm):
Bài 1
Hướng dẫn:
Thực hiện phép tính với số hữu tỉ, giá trị tuyệt đối của một số hữu tỉ.
Cách giải:
|
a) \(\dfrac{7}{2}.\dfrac{{11}}{6} – \dfrac{7}{2}.\dfrac{5}{6}\) \(\begin{array}{l} = \dfrac{7}{2}.\left( {\dfrac{{11}}{6} + \dfrac{5}{6}} \right)\\ = \dfrac{7}{2}.\dfrac{{16}}{6}\\ = \dfrac{{28}}{3}\end{array}\) |
b) \(\sqrt {36} – 3.\sqrt {\dfrac{1}{4}} + \left| {\dfrac{{ – 3}}{2}} \right|\) \(\begin{array}{l} = 6 – 3.\dfrac{1}{2} + \dfrac{3}{2}\\ = 6 + \left( {\dfrac{3}{2} – \dfrac{3}{2}} \right)\\ = 6 + 0 = 6\end{array}\) |
c) \({\left( {\dfrac{{ – 1}}{2}} \right)^3} – \dfrac{7}{8}:\dfrac{7}{4} + \left| {\dfrac{{ – 9}}{8}} \right| + \sqrt {81} \) \(\begin{array}{l} = \dfrac{{ – 1}}{8} – \dfrac{7}{8}.\dfrac{4}{7} + \dfrac{9}{8} + 9\\ = \left( { – \dfrac{1}{8} + \dfrac{9}{8}} \right) – \dfrac{1}{2} + 9\\ = 1 – \dfrac{1}{2} + 9\\ = \dfrac{1}{2} + 9 = \dfrac{{19}}{2}\end{array}\) |
Bài 2
Hướng dẫn:
Thực hiện phép tính với số hữu tỉ, giá trị tuyệt đối của một số hữu tỉ.
Cách giải:
|
a) \(\dfrac{3}{5}x – \dfrac{6}{7} = \dfrac{1}{7}\) \(\begin{array}{l}\dfrac{3}{5}x = \dfrac{1}{7} + \dfrac{6}{7}\\\dfrac{3}{5}x = \dfrac{7}{7} = 1\\x = 1:\dfrac{3}{5}\\x = \dfrac{5}{3}\end{array}\) Vậy \(x = \dfrac{5}{3}\) |
b) \({\left( {2x – 1} \right)^3} = 64\) \(\begin{array}{l}{\left( {2x – 1} \right)^3} = {4^3}\\2x – 1 = 4\\2x = 4 + 1\\2x = 5\\x = \dfrac{5}{2}\end{array}\) Vậy \(x = \dfrac{5}{2}\)
|
c) \(2\left| {x + 1} \right| – 0,5 = \sqrt {\dfrac{1}{9}} \) \(\begin{array}{l}2\left| {x + 1} \right| – \dfrac{1}{2} = \dfrac{1}{3}\\2\left| {x + 1} \right| = \dfrac{1}{3} + \dfrac{1}{2}\\2\left| {x + 1} \right| = \dfrac{{2 + 3}}{6} = \dfrac{5}{6}\\\left| {x + 1} \right| = \dfrac{5}{6}:2\\\left| {x + 1} \right| = \dfrac{5}{{12}}\end{array}\) Trường hợp 1: \(x + 1 = \dfrac{5}{{12}} \Rightarrow x = \dfrac{5}{{12}} – 1 = \dfrac{{ – 7}}{{12}}\) Trưởng hợp 2: \(x + 1 = \dfrac{{ – 5}}{{12}} \Rightarrow x = \dfrac{{ – 5}}{{12}} – 1 = \dfrac{{ – 17}}{{12}}\) Vậy \(x = \dfrac{{ – 7}}{{12}};x = \dfrac{{ – 17}}{{12}}\) |
Bài 3
Hướng dẫn:
a) Chứng minh \(\Delta OAM = \Delta OBM\left( {c.c.c} \right)\)
b) Chứng minh \(\Delta OAH = \Delta OBH\left( {c.g.c} \right) \Rightarrow HA = HB\) (hai cạnh tương ứng)
c) Chứng minh \(\Delta OHK = \Delta OHE\left( {c.g.c} \right)\)
Suy ra, \(HK = HE \Rightarrow H\) là trung điểm của \(EK\,\,\,\left( 1 \right)\)
\(\angle OHK = \angle OHE\)\( \Rightarrow OH \bot EK\) tại \(H\,\,\,\left( 2 \right)\)
Từ (1) và (2), suy ra \(OH\) là đường trung trực của \(EK\).
d) Chứng minh \(\Delta OAK = \Delta OBE\left( {c.g.c} \right)\) từ đó chứng minh được \(\angle NBK = \angle NAE\)
Chứng minh \(\Delta NBK = \Delta NHE\left( {c.c.c} \right) \Rightarrow \angle NHK = \angle NHE\) từ đó chứng minh được \(NH \bot EK\) tại \(H\)
Cách giải:
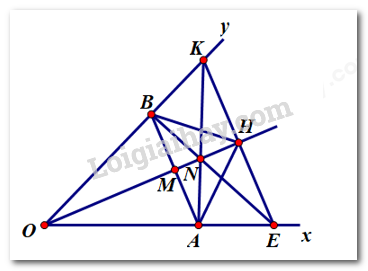
a) \(M\) là trung điểm của \(AB \Rightarrow MA = MB\)
Xét \(\Delta OAM\) và \(\Delta OBM\) có:
\(\left. \begin{array}{l}OM\,\,\,chung\\OA = OB\left( {gt} \right)\\MA = MB\left( {cmt} \right)\end{array} \right\} \Rightarrow \Delta OAM = \Delta OBM\left( {c.c.c} \right)\)
b) \(\Delta OAM = \Delta OBM\left( {cmt} \right) \Rightarrow \angle AOM = \angle BOM\) (hai góc tương ứng)
Xét \(\Delta OAH\) và \(\Delta OBH\) có:
\(\left. \begin{array}{l}OH\,\,\,chung\\\angle AOM = \angle BOM\left( {cmt} \right)\\OA = OB\left( {gt} \right)\end{array} \right\} \Rightarrow \Delta OAH = \Delta OBH\left( {c.g.c} \right) \Rightarrow HA = HB\) (hai cạnh tương ứng)
c) Ta có: \(OA = OB\left( {gt} \right) \Rightarrow \Delta OAB\) cân tại \(O \Rightarrow \angle OAB = \angle OBA\)
Vì \(AB\)//\(EK\), suy ra: \(\angle OBA = \angle OKE\) (hai góc ở vị trí đồng vị) và \(\angle OAB = \angle OEK\) (hai góc ở trí đồng vị)
Từ đó, suy ra \(\angle OKE = \angle OEK \Rightarrow \Delta OEK\) cân tại \(O \Rightarrow OK = OE\)
Xét \(\Delta OHK\) và \(\Delta OHE\) có:
\(\left. \begin{array}{l}OK = OE\left( {cmt} \right)\\\angle KOH = \angle EOH\,\left( {do\,\,\angle BOM = \angle AOM} \right)\\OH\,\,chung\end{array} \right\} \Rightarrow \Delta OHK = \Delta OHE\left( {c.g.c} \right)\)
Suy ra,
+ \(HK = HE\) (hai cạnh tương ứng) \( \Rightarrow H\)là trung điểm của \(EK\,\,\,\left( 1 \right)\)
+ \(\angle OHK = \angle OHE\) (hai góc tương ứng) mà \(\angle OHK + \angle OHE = {180^0}\) nên \(\angle OHK = \angle OHE = \dfrac{{{{180}^0}}}{2} = {90^0}\), do đó \(OH \bot EK\) tại \(H\,\,\,\left( 2 \right)\)
Từ (1) và (2), suy ra \(OH\) là đường trung trực của \(EK\).
d) Ta có: \(AE = OE – OA\,;\,\,BK = OK – OB\) mà \(OE = OK\,;\,\,OA = OB\)
Suy ra, \(AE = BK\)
Xét \(\Delta OAK\) và \(\Delta OBE\) có:
\(\left. \begin{array}{l}OA = OB\left( {cmt} \right)\\\angle O\,\,chung\\OK = OH\left( {cmt} \right)\end{array} \right\} \Rightarrow \Delta OAK = \Delta OBE\left( {c.g.c} \right)\)
Suy ra, \(\angle OKA = \angle OEB\) và \(\angle OAH = \angle OBE\) (hai góc tương ứng)
Ta có: \(\left\{ \begin{array}{l}\angle NBK = {180^0} – \angle OBE\\\angle NAE = {180^0} – \angle OAK\end{array} \right.\)
Do đó, \(\angle NBK = \angle NAE\)
Xét \(\Delta NBK\) và \(\Delta NHE\) có:
\(\left. \begin{array}{l}\angle NBK = \angle NAE\left( {cmt} \right)\\BK = AE\left( {cmt} \right)\\\angle OKA = \angle OEB\left( {cmt} \right)\end{array} \right\} \Rightarrow \Delta NBK = \Delta NHE\left( {c.c.c} \right) \Rightarrow \angle NHK = \angle NHE\) (hai góc tương ứng)
Mà \(\angle NHK + \angle NHE = {180^0}\)
\( \Rightarrow \angle NHK = \angle NHE = \dfrac{{{{180}^0}}}{2} = {90^0}\)
\( \Rightarrow NH \bot EK\) tại \(H\) mà \(OH \bot EK\) tại \(H\)
\( \Rightarrow NH \equiv OH\)
\( \Rightarrow O,N,H\) thẳng hàng
\( \Rightarrow O,M,H\) thẳng hàng.
Bài 4
Hướng dẫn:
Đánh giá các số hạng của tổng để tìm giá trị nhỏ nhất của \(A\).
Chú ý: \({x^2} \ge 0,\forall x \in \mathbb{R}\).
Cách giải:
Ta có: \({x^2} \ge 0;\sqrt x \ge 0\) với mọi số thực \(x \ge 0\) nên \({x^2} + 3\sqrt x \ge 0\) với mọi số thực \(x \ge 0\).
Suy ra \({x^2} + 3\sqrt x – 2024 \ge – 2024\) với mọi số thực \(x \ge 0.\) Hay \(A \ge – 2024\) với mọi số thực \(x \ge 0.\)
Dấu “=” xảy ra \( \Leftrightarrow x = 0\).
Vậy \(\min A = – 2024 \Leftrightarrow x = 0\).