Hướng dẫn giải Đề bài Đề thi học kì 1 – Đề số 7 – Đề thi đề kiểm tra Toán lớp 7 Kết nối tri thức.
Câu hỏi/Đề bài:
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Số đối của \(\dfrac{{ – 7}}{{12}}\) là:
A. \(\dfrac{7}{{12}}\) B. \(\dfrac{7}{{ – 12}}\) C. \(\dfrac{{12}}{{ – 7}}\) D. \(\dfrac{{12}}{7}\)
Câu 2: Chọn khẳng định đúng.
A. \(\dfrac{{ – 37}}{{41}} > \dfrac{{23}}{{ – 17}}\) B. \({\left( {\dfrac{1}{3}} \right)^{12}} > {\left( {\dfrac{1}{3}} \right)^{10}}\) C. \({\left( {2,5} \right)^6} = {\left( {0,5} \right)^{12}}\) D. \({\left( {2,5} \right)^4} < {\left( { – 2,5} \right)^5}\)
Câu 3: Chọn đáp án sai. Nếu \(\sqrt x = \dfrac{2}{3}\) thì:
A. \(x = {\left( { – \dfrac{2}{3}} \right)^2}\) B. \(x = – {\left( { – \dfrac{2}{3}} \right)^2}\) C. \(x = \dfrac{4}{9}\) D. \(x = {\left( {\dfrac{2}{3}} \right)^2}\)
Câu 4: Trong các phát biểu sau, phát biểu nào sai?
A. Giá trị tuyệt đối của một số thực là một số dương hoặc bằng 0.
B. Hai số có giá trị tuyệt đối bằng nhau là hai số bằng nhau hoặc đối nhau.
C. Hai số đối nhau có giá trị tuyệt đối bằng nhau.
D. Giá trị tuyệt đối của một số thực luôn bằng chính nó.
Câu 5: Quan sát Hình 2, có \(IK//EF\). Hãy tính giá trị của \(x\)?
A. \(x = {70^0}\) B. \(x = {110^0}\) C. \(x = {120^0}\) D. \(x = {90^0}\)
Câu 6:
Cho tam giác \(ABC\) có \(AB < AC\). Tia phân giác của góc \(A\) cắt \(BC\) ở \(K\). Từ \(B\) kẻ đường vuông góc với \(AK\) tại \(H\) cắt \(AC\) ở \(D\). Chọn câu sai.
A. \(HB = AD\) B. \(HB = HD\) C. \(AB = AD\) D. \(\widehat {ABH} = \widehat {ADH}\)
Câu 7: Số học sinh đăng ký học bổ trợ các Câu lạc bộ Toán, Ngữ văn, Tiếng anh của lớp 7 của một trường được biểu diễn qua biểu đồ hình quạt tròn như sau:
Tính số phần trăm học sinh đăng ký môn Toán là bao nhiêu?
A. 40% B. 37,5% C. 30% D. 35%
Câu 8: Cho biểu đồ biểu diễn chiều cao trung bình của nam và nữ ở một số quốc gia châu Á:
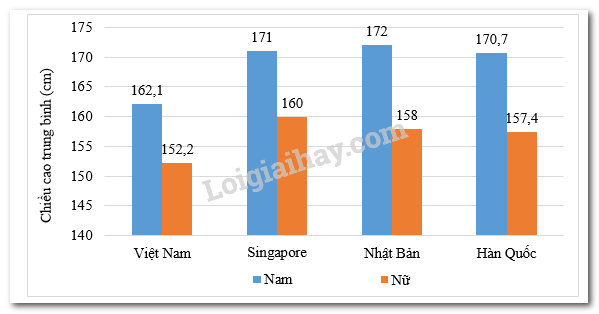
Sự chênh lệch chiều cao giữa nam và nữ của nước nào là lớn nhất?
- Việt Nam B. Singapore C. Nhật Bản D. Hàn Quốc
Câu 9: Phát biểu định lí sau bằng lời:
|
GT |
\(a//b,c \bot a\) |
|
KL |
\(c \bot b\) |
A. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
B. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.
C. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \({60^0}\).
D. Cả A, B, C đều đúng.
Câu 10: Vẽ \(\angle xOy = {50^0}\). Vẽ tia \(Om\) là tia phân giác của góc \(xOy\). Vẽ tia \(On\) là tia đối của tia \(Ox\). Tính góc \(mOn\).
A. \(\angle mOn = {125^0}\) B. \(\angle mOn = {155^0}\) C. \(\angle mOn = {160^0}\) D. \(\angle mOn = {175^0}\)
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính:
a) \(\dfrac{7}{2}.\dfrac{{11}}{6} – \dfrac{7}{2}.\dfrac{5}{6}\)
b) \(\sqrt {36} – 3.\sqrt {\dfrac{1}{4}} + \left| {\dfrac{{ – 3}}{2}} \right|\)
c) \({\left( {\dfrac{{ – 1}}{2}} \right)^3} – \dfrac{7}{8}:\dfrac{7}{4} + \left| {\dfrac{{ – 9}}{8}} \right| + \sqrt {81} \)
Bài 2 (2,0 điểm). Tìm \(x\):
a) \(\dfrac{3}{5}x – \dfrac{6}{7} = \dfrac{1}{7}\)
b) \({\left( {2x – 1} \right)^3} = 64\)
c) \(2\left| {x + 1} \right| – 0,5 = \sqrt {\dfrac{1}{9}} \)
Bài 3: (3,5 điểm)
Cho góc nhọn \(xOy\), lấy điểm \(A\) trên tia \(Ox\) (điểm\(A\) khác \(O\)) và điểm \(B\) trên tia \(Oy\) sao cho \(OA = OB\). Gọi \(M\) là trung điểm của \(AB\).
a) Chứng minh: \(\Delta OAM = \Delta OBM\)
b) Trên tia \(OM\) lấy điểm \(H\) sao cho \(OM < OH\). Chứng minh \(HA = HB\).
c) Qua \(H\) kẻ đường thẳng song song với \(AB\) cắt \(Ox\) tại \(E\) cắt \(Oy\) tại \(K\). Chứng minh \(OH\) là đương trung trực của \(EK\).
d) Gọi giao điểm của \(AK\) và \(BE\) là \(N\). Chứng minh ba điểm \(O,M,N\) thẳng hàng.
Bài 4: (0,5 điểm)
Tìm giá trị nhỏ nhất của biểu thức \(A = {x^2} + 3\sqrt x – 2024\) với \(x \ge 0\).