Đáp án Lời giải Đề thi giữa kì 2 – Đề số 1 – Đề thi đề kiểm tra Toán lớp 7 Kết nối tri thức.
Câu hỏi/Đề bài:
I. Trắc nghiệm:
|
1. C |
2. D |
3. A |
4. A |
|
5. C |
6. D |
7. C |
8. C |
Câu 1:
Hướng dẫn:
Trong tam giác cân, đường trung tuyến ứng với đỉnh cân đồng thời là đường trung trực, đường cao, đường phân giác.
Cách giải:
Tam giác ABC cân tại B nên đường trung tuyến BN đồng thời là đường phân giác.
Chọn C.
Câu 2:
Hướng dẫn:
Dựa vào mối quan hệ giữa góc và cạnh trong tam giác để so sánh các cạnh với nhau.
Cách giải:
Ta có: \(\angle C = {180^0} – \left( {{{50}^0} + {{90}^0}} \right) = {40^0}\).
\( \Rightarrow \angle C < \angle A < \angle B\)
\( \Rightarrow AB < BC BC > AB\).
Chọn D.
Câu 3:
Hướng dẫn:
Tính chất hai đại lượng tỉ lệ thuận
Cách giải:
\(x\) và \(y\) là hai đại lượng tỉ lệ thuận \( \Rightarrow y = ax\left( {a \ne 0} \right)\)
Thay \(x = 5;y = 10\) vào ta được: \(10 = a.5 \Rightarrow a = 2\)
Vậy hệ số tỉ lệ của \(y\) đối với \(x\) là \(a = 2\).
Ta có: \(y = 2x\), khi \(x = 2\) thì \(y = 2.2 = 4\).
Chọn A.
Câu 4:
Hướng dẫn:
Tính chất hai đại lượng tỉ lệ nghịch: tích 2 giá trị tương ứng của 2 đại lượng luôn không đổi (bằng hệ số tỉ lệ)
Cách giải:
Hệ số tỉ lệ là: -21 . 12 = -252.
Khi x = 7 thì y = -252 : 7 = -36.
Chọn A
Câu 5:
Hướng dẫn:
Mô tả
Cách giải:
Tổng lập phương của hai số x và y là x3 + y3
Câu 6:
Hướng dẫn:
Hệ số cao nhất của đa thức là hệ số của hạng tử có bậc cao nhất trong đa thức.
Cách giải:
Đa thức M = 10x2 – 4x + 3 – 5x5 có hệ số cao nhất là -5.
Chọn D
Chú ý: Hệ số cao nhất không phải hệ số lớn nhất trong đa thức.
Câu 7:
Hướng dẫn:
Nếu \(\Delta ABC\) có trung tuyến \(AM\) và trọng tâm \(G\) thì \(AG = \dfrac{2}{3}AM\).
Cách giải:
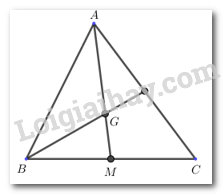
Nếu \(\Delta ABC\) có trung tuyến \(AM\) và trọng tâm \(G\) thì \(GM = \dfrac{1}{3}AM = \dfrac{1}{3}.9 = 3(cm)\).
Chọn C.
Câu 8:
Hướng dẫn:
Bất đẳng thức tam giác: Kiểm tra tổng độ dài 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất không. Nếu không thì bộ 3 độ dài đó không tạo được thành tam giác.
Cách giải:
Vì 1 + 2 = 3 nên không thỏa mãn bất đẳng thức tam giác.
Chọn C.
II. TỰ LUẬN
Bài 1:
Phương pháp:
a) Thực hiện các phép toán với phân số.
b) Vận dụng định nghĩa hai phân số bằng nhau: Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \(ad = bc\).
Cách giải:
a) \(\dfrac{1}{{12}} + x = \dfrac{{ – 11}}{{12}}\)
\(\begin{array}{l}x = \dfrac{{ – 11}}{{12}} – \dfrac{1}{{12}}\\x = \dfrac{{ – 11 – 1}}{{12}}\\x = \dfrac{{ – 12}}{{12}} = – 1\end{array}\)
Vậy \(x = – 1\)
b) \(\dfrac{{2x – 1}}{{27}} = \dfrac{3}{{2x – 1}}\)
\(\begin{array}{l}{\left( {2x – 1} \right)^2} = 27.3 = 81\\{\left( {2x – 1} \right)^2} = {\left( { \pm 9} \right)^2}\end{array}\)
|
Trường hợp 1: \(\begin{array}{l}2x – 1 = 9\\2x = 10\\x = 5\end{array}\) |
Trường hợp 2: \(\begin{array}{l}2x – 1 = – 9\\2x = – 8\\x = – 4\end{array}\) |
Vậy \(x \in\){ 5; – 4}
Bài 2:
Hướng dẫn:
Gọi số công nhân của 3 đội lần lượt là \(x,y,z\) (điều kiện: \(x,y,z \in {\mathbb{N}^*}\))
Vận dụng kiến thức về tỉ lệ nghịch để tìm các đại lượng của đề bài.
Cách giải:
Gọi số công nhân của 3 đội lần lượt là \(x,y,z\) (điều kiện: \(x,y,z \in {\mathbb{N}^*}\))
Vì đội I có nhiều hơn đội II là \(4\) người nên: \(x – y = 4\)
Vì số năng suất mỗi người là như sau, nên số người và số ngày hoàn thành công việc là hai đại lượng tỉ lệ nghịch, nên ta có:
\(4x = 6y = 8z\) hay \(\dfrac{x}{{\dfrac{1}{4}}} = \dfrac{y}{{\dfrac{1}{6}}} = \dfrac{z}{{\dfrac{1}{8}}}\)
Theo tính chất của dãy tỉ số bằng nhau, ta có: \(\dfrac{x}{{\dfrac{1}{4}}} = \dfrac{y}{{\dfrac{1}{6}}} = \dfrac{z}{{\dfrac{1}{8}}} = \dfrac{{x – y}}{{\dfrac{1}{4} – \dfrac{1}{6}}} = \dfrac{4}{{\dfrac{1}{{12}}}} = 48\)
Từ \(\dfrac{x}{{\dfrac{1}{4}}} = 48 \Rightarrow x = 12\) (tmđk)
\(\dfrac{y}{{\dfrac{1}{6}}} = 48 \Rightarrow y = 8\) (tmđk)
\(\dfrac{z}{{\dfrac{1}{8}}} = 48 \Rightarrow z = 6\) (tmđk)
Vậy số công nhân của \(3\) đội lần lượt là: \(12\) công nhân, \(8\) công nhân, \(6\) công nhân.
Bài 3:
Hướng dẫn:
a) Thu gọn và sắp xếp các hạng tử của đa thức \(A\left( x \right),\,B\left( x \right)\) theo lũy thừa giảm dần của biến.
b) Tính \(A\left( x \right) + B\left( x \right);\,A\left( x \right) – B\left( x \right)\).
c) Chứng minh rằng đa thức \(C\left( x \right)\) không có nghiệm.
Cách giải:
a) Thu gọn:
\(\begin{array}{l}A\left( x \right) = 2\,{x^4} – 5\,{x^3} + 7\,x – 5 + 4\,{x^3} + 3\,{x^2} + 2\,x + 3\\A\left( x \right) = 2\,{x^4} + \left( { – 5\,{x^3} + 4\,{x^3}} \right) + 3{x^2} + \left( {7\,x + 2\,x} \right) – 5 + 3\\A\left( x \right) = 2\,{x^4} – {x^3} + 3\,{x^2} + 9\,x\, – 2\end{array}\)
\(\begin{array}{l}B\left( x \right) = 5\,{x^4} – 3\,{x^3} + 5\,x – 3\,{x^4} – 2\,{x^3}\, + 9 – 6\,x\\B\left( x \right) = \left( {5\,{x^4} – 3\,{x^4}} \right) + \left( { – 3\,{x^3} – 2\,{x^3}} \right) + \left( {5\,x – 6\,x} \right) + 9\\B\left( x \right) = \,\,\,\,\,\,2\,{x^4}\, – \,5{x^3} – x + 9\end{array}\)
b) Tính \(A\left( x \right) + B\left( x \right);\,A\left( x \right) – B\left( x \right)\).
\(\begin{array}{l} + )\,A\left( x \right) + B\left( x \right) = \left( {2\,{x^4} – {x^3} + 3\,{x^2} + 9\,x – 2} \right) + \left( {2\,{x^4} – 5\,{x^3} – x + 9} \right)\\ = \left( {2\,{x^4} + 2\,{x^4}} \right) + \left( { – {x^3} – 5\,{x^3}} \right) + 3\,{x^2} + \left( {9\,x – x} \right) + \left( { – 2 + 9} \right)\\ = \,\,\,4\,{x^4} – 6\,{x^3} + 3\,{x^2} + 8\,x + 7\end{array}\)
\(\begin{array}{l} + )\,A\left( x \right) – B\left( x \right) = \left( {2\,{x^4} – {x^3} + 3\,{x^2} + 9\,x – 2} \right) – \left( {2\,{x^4} – 5\,{x^3} – x + 9} \right)\\ = \left( {2\,{x^4} – \,{x^3} + 3\,{x^2} + 9\,x – 2} \right) – 2\,{x^4} + 5\,{x^3} + x – 9\\ = \left( {2\,{x^4} – \,2\,{x^4}} \right) + \left( { – {x^3} + 5\,{x^3}} \right) + 3\,{x^2} + \left( {9\,x + x} \right) + \left( { – 2 – 9} \right)\\ = \,\,\,\,\,\,\,\,\,\,4\,{x^3} + \,3\,{x^2} + 10\,x – 11\end{array}\)
c) Chứng minh rằng đa thức \(C\left( x \right)\) không có nghiệm.
Ta có: \(C\left( x \right) = {x^4} + 4\,{x^2} + 5\).
Vì \({x^4}\, > 0,\,\,\forall \,x\) và \({x^2} > 0,\,\forall \,x\) nên \(C\left( x \right) > 0,\,\,\forall \,x.\)
\( \Rightarrow \) không có giá trị nào của \(x\) làm cho \(C\left( x \right) = 0\).
\( \Rightarrow \,C\left( x \right)\) là đa thức không có nghiệm.
Bài 4: Phương pháp:
a) Chứng minh hai tam giác bằng nhau theo trường hợp c.g.c.
b) Chứng minh \(\Delta ABD\)là tam giác cân có một góc bằng \({60^0}\), rồi suy ra \(\Delta ABD\) là tam giác đều.
c) Chứng minh \(DE = DH\) (hai cạnh tương ứng). Mà \(DH = DB\) (giả thiết) \( \Rightarrow DE = DB\).
d) Chứng minh \(FD//AB\) rồi sau đó chứng minh \(DI//AB\), rồi suy ra \(I,\,D,\,F\) là ba điểm thẳng hàng. Cách giải:
|
a) Xét \(\Delta AHB\) và \(\Delta AHD\) ta có: \(HD = HB\) (gt) \(AH\,\,chung\) \(\angle AHB = \angle AHD = {90^0}\) \( \Rightarrow \)\(\Delta AHB = \,\Delta AHD\) (c.g.c) b) \(\Delta ABC\) vuông tại \(A\), có \(\angle C = {30^0} \Rightarrow \angle B = {90^0} – {30^0} = {60^0}\) (định lý tổng ba góc của một tam giác). Vì \(\Delta AHB = \,\Delta AHD\) (cmt) \( \Rightarrow AB = AD\) (hai cạnh tương ứng). \( \Rightarrow \Delta ABD\) cân tại \(A\) mà \(\angle B = {60^0}\) Do đó: \(\Delta ABD\)là tam giác đều. c) Vì \(\Delta ABD\)là tam giác đều (cmt) \( \Rightarrow \angle DAB = {60^0}\) \(\begin{array}{l} \Rightarrow \angle CAD = {90^0} – \angle DAB\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {90^0} – {60^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {30^0}\end{array}\) Xét \(\Delta ACD\) có \(\angle ACD = \angle \,CAD = {30^0}\). \( \Rightarrow \Delta ACD\) cân tại \(D.\) \( \Rightarrow \,CD = AD\) Xét \(\Delta DEC\) và \(\Delta DHA\) có: \(CD = AD\,\,\left( {cmt} \right)\) \(\angle E = \angle H = {90^0}\) \(\angle CDE = \angle ADH\) (đối đỉnh) \( \Rightarrow \,\Delta DEC = \Delta DHA\) (cạnh huyền – góc nhọn). \( \Rightarrow DE = DH\) (hai cạnh tương ứng). Mà \(DH = DB\) (giả thiết) \( \Rightarrow DE = DB\). d) Từ \(D\) kẻ \(DF\) vuông góc với \(AC\) (\(F\,\)thuộc \(AC\)), \(I\) là giao điểm của \(CE\) và \(AH.\) Chứng minh ba điểm \(I,\,D,\,F\) thẳng hàng. Ta có: \(\begin{array}{l}DF \bot AC\,\left( {gt} \right)\\AB \bot AC\left( {gt} \right)\\ \Rightarrow DF//AB\,\,\,\,\,\,\,\left( 1 \right)\end{array}\) Ta lại có: \(\angle FDC = \angle HDI\) (đối đỉnh) Mà \(\angle FDC = {90^0} – \angle C = {90^0} – {30^0} = {60^0}\) \( \Rightarrow \angle FDC = \angle HDI = {60^0}\) Mà \(\angle B = {60^0}\) \( \Rightarrow \angle B = \angle DHI\) Mà hai góc này ở vị trí so le trong Do đó: \(DI//AB\) (2) Từ (1) và (2), suy ra: \(\angle I,D,B\) là ba điểm thẳng hàng. |
Câu 5:
Hướng dẫn:
Vận dụng định nghĩa hai phân số bằng nhau để chứng minh.
Cách giải:
Ta có: \(\dfrac{1}{c} = \dfrac{1}{2}\left( {\dfrac{1}{a} + \dfrac{1}{b}} \right)\)
\(\begin{array}{l} \Rightarrow \dfrac{1}{c} = \dfrac{{a + b}}{{2ab}}\\ \Rightarrow 2ab = ac + bc\\ \Rightarrow ab + ab = ac + bc\\ \Rightarrow ab – bc = ac – ab\\ \Rightarrow b\left( {a – c} \right) = a\left( {c – b} \right)\end{array}\)
\( \Rightarrow \dfrac{a}{b} = \dfrac{{a – c}}{{c – b}}\) (đpcm)