Đáp án Đề bài Đề thi học kì 1 – Đề số 8 – Đề thi đề kiểm tra Toán lớp 7 Chân trời sáng tạo.
Câu hỏi/Đề bài:
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Kết quả của phép tính: \(\dfrac{1}{2} + {\left[ {{{\left( { – 1103} \right)}^{1999}}} \right]^0}\) là:
A. \(\dfrac{1}{2}\) B. \(1\dfrac{1}{2}\) C. \(1\) D. \(\dfrac{{ – 1}}{2}\)
Câu 2: Số nào dưới đây là số vô tỉ?
A. \(\sqrt 7 \) B. \(1,\left( {01} \right)\) C. \(\sqrt {16} \) D. \(\dfrac{{ – 1}}{7}\)
Câu 3: Kim tự tháp Kheops là công trình kiến trúc nổi tiếng thể giới. Để xây dựng được công trình này, người ta phải sử dụng tới hơn 2,5 triệu mét khối đá, với diện tích đáy lên tới 52 198,16 \({m^2}\). (Theo khoahoc.tv)
Biết rằng đáy của kim tự tháp Kheops có dạng một hình vuông. Tính độ dài cạnh đáy của kim tự tháp này (làm tròn kết quả đến chữ số thập phân thứ nhất).
A. \(229,5m\) B. \(229m\) C. \(228,5m\) D. \(228m\)
Câu 4: Kết quả của phép tính: \(\left| {5 – \sqrt {45} } \right| + 15 – \sqrt {45} \) là:
A. \(10\) B. \(20 – 2\sqrt {45} \) C. \(20\) D. \(10 – \sqrt {45} \)
Câu 5: Cho biểu đồ
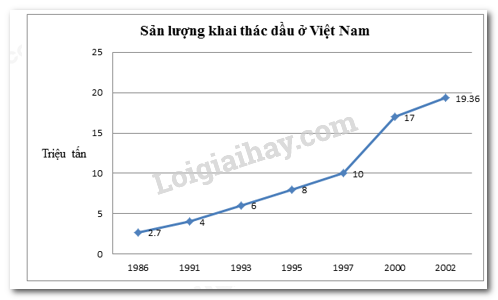
Hãy cho biết sản lượng khai thác dầu ở Việt Nam giai đoạn nào tăng nhiều nhất?
A. \(1986 – 1991\) B. \(1991 – 1993\) C. \(1997 – 2000\) D. \(2000 – 2002\)
Câu 6: Cho hình lăng trụ đứng có đáy là hình thang với đáy bé bằng \(5\,cm,\) đáy lớn bằng \(7\,cm\) và hai cạnh bên lần lượt bằng \(3\,cm;\,4cm.\) Biết chiều cao của hình lăng trụ đứng đó là \(8\,cm.\) Diện tích xung quanh của hình lăng trụ đứng đó là:
A. \(152\,c{m^2}\) B. \(76\,c{m^2}\) C. \(159\,c{m^2}\) D. \(159\,cm\)
Câu 7: Cho \(\angle xOy = 90^\circ \). Trên \(Ox\) lấy \(OA = 4cm\), trên \(Oy\) lấy \(OB = 2,5cm\). Qua \(A\) kẻ đường thẳng vuông góc với \(Ox\). Qua \(B\) kẻ đường thẳng vuông góc với \(Oy\). Hai đường thẳng đó giao nhau tại \(C\). Tính số đo góc ?
A. B. C. D.
Câu 8: Tỉ lệ phần trăm số học sinh xuất sắc, giỏi, khá, trung bình của một lớp được biểu diễn qua biểu đồ hình quạt tròn sau:
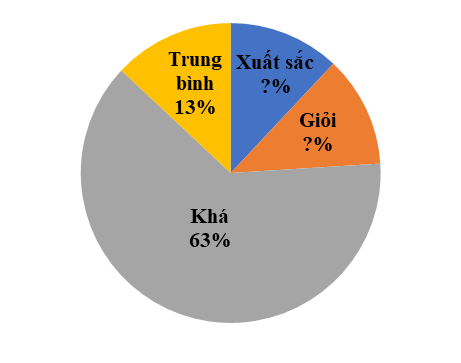
Tìm tỉ số phần trăm số học sinh xuất sắc và số học sinh giỏi của lớp đó, biết rằng số học sinh xuất sắc bằng số học sinh giỏi.
A. Số học sinh xuất sắc chiếm , số học sinh giỏi chiếm .
B. Số học sinh xuất sắc chiếm , số học sinh giỏi chiếm .
C. Số học sinh xuất sắc chiếm , số học sinh giỏi chiếm .
D. Số học sinh xuất sắc chiếm \(12\% \), số học sinh giỏi chiếm \(12\% \).
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính:
a) \(\dfrac{{ – 8}}{{19}}.\dfrac{{16}}{{31}} + \dfrac{{ – 8}}{{19}}.\dfrac{{15}}{{31}} – \dfrac{{11}}{{19}}\) b) \(\sqrt {{{\left( { – 5} \right)}^2}} .{\left( { – \dfrac{1}{5}} \right)^2}:\left[ {{{\left( {\dfrac{{ – 1}}{3}} \right)}^2} + \sqrt {\dfrac{1}{4}} – \sqrt {\dfrac{{16}}{9}} } \right]\)
c) \(\sqrt {121} – \sqrt {225} + \sqrt {\dfrac{{25}}{4}} \) d) \(\left| {\dfrac{{ – 11}}{3}} \right| + {\left( {\dfrac{{ – 1}}{2}} \right)^2} – \left| {4\dfrac{1}{2} + \left( { – 3,25} \right)} \right|\)
Bài 2: (2,0 điểm)
Tìm \(x\), biết:
a) \(\left( {3{x^2} + 1} \right)\left( {4x + \dfrac{1}{3}} \right) = 0\) b) \({\left( {x – \dfrac{3}{5}} \right)^2} = \dfrac{4}{3}:\dfrac{1}{3}\)
c) \(\left( {x + 2.\sqrt {16} } \right).\left| {2x + 3} \right| = 0\) d) \(\left| {x – \dfrac{2}{3}} \right| – 0,75 = 1\dfrac{1}{4}\)
Bài 3: (1,5 điểm) Trong hình vẽ bên dưới có \(BE//AC,CF//AB\). Biết \(\angle A = {80^0},\angle ABC = {60^0}.\)
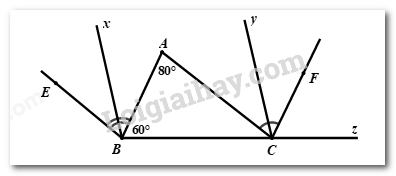
a) Chứng minh rằng \(\angle ABE = \angle ACF\);
b) Tính số đo của các góc \(BCF\) và \(ACB\).
c) Gọi \(Bx,Cy\) lần lượt là tia phân giác của các góc \(ABE\) và \(ACF\). Chứng minh rằng \(Bx//Cy\).
Bài 4: (1,0 điểm) Một chiếc bình có dạng hình hộp chữ nhật có kích thước đáy là \(10\,cm\) và \(15\,cm.\) Biết diện tích xung quanh bằng tổng diện tích hai đáy. Người ta đổ một lượng nước vào bình. Tính thể tích lượng nước được đổ vào bình biết mực nước cao bằng \(\dfrac{2}{3}\) chiều cao của bình.
Bài 5: (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức:
\(A = \sqrt {{{(x + 2)}^4} + 25} + {\left( {1 – y} \right)^2} – 999\)