Trả lời Lời giải Đề thi giữa kì 2 – Đề số 3 – Đề thi đề kiểm tra Toán lớp 7 Cánh diều.
Câu hỏi/Đề bài:
I. Trắc nghiệm
|
1.C |
2.C |
3. B |
4.A |
|
5.C |
6.B |
7.C |
8.C |
Câu 1:
Hướng dẫn:
Nếu \(\Delta ABC\) có trung tuyến \(AM\) và trọng tâm \(G\) thì \(AG = \dfrac{2}{3}AM\).
Cách giải:
Nếu \(\Delta ABC\) có trung tuyến \(AM\) và trọng tâm \(G\) thì \(AG = \dfrac{2}{3}AM;GM = \dfrac{1}{3}AM;AG = 2GM\)
Chọn B.
Câu 2:
Hướng dẫn:
Mô tả biểu đồ hình quạt tròn.
Cách giải:
Cả hình tròn biểu diễn 100% do đó, khẳng định “Cả hình tròn biểu diễn 75%” là không đúng.
Chọn C.
Câu 3:
Hướng dẫn:
Sử dụng tính chất tia phân giác của góc và định lí tổng 3 góc trong một tam giác.
Cách giải:
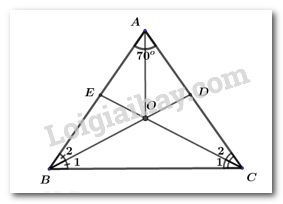
Ta có: \(\widehat {BOC} = {180^^\circ }{\rm{ \;}} – \widehat {{B_1}} – \widehat {{C_1}}\).
Vì BD và CE lần lượt là các tia phân giác của góc B và C nên ta có: \(\widehat {{B_1}} = \dfrac{{\hat B}}{2};{\mkern 1mu} \widehat {{C_1}} = \dfrac{{\hat C}}{2}\).
Trong tam giác ABC ta có: \(\hat B + \hat C = {180^^\circ }{\rm{ \;}} – \hat A = {180^^\circ }{\rm{ \;}} – {70^^\circ }{\rm{ \;}} = {110^^\circ }\).
\( \Rightarrow \widehat {BOC} = {180^^\circ }{\rm{ \;}} – \widehat {{B_1}} – \widehat {{C_1}} = {180^^\circ }{\rm{ \;}} – \dfrac{{\hat B + \hat C}}{2} = {180^^\circ }{\rm{ \;}} – {55^^\circ }{\rm{ \;}} = {125^^\circ }\)
Chọn B.
Câu 4:
Hướng dẫn:
+ Mọi điểm nằm trên đường phân giác của một góc thì cách đều hai cạnh của góc.
+ Giao của ba đường phân giác trong tam giác cách đều ba cạnh của tam giác đó.
+ Giao điểm của ba đường phân giác trong tam giác là tâm đường tròn nội tiếp của tam giác đó.
Cách giải:
Gọi \(I\) là giao điểm của ba đường phân giác của tam giác thì \(I\)cách đều ba cạnh của tam giác.
Chọn A.
Câu 5
Hướng dẫn:
+ Tam giác cân có hai góc ở đáy bằng nhau.
+ Tam giác cân có hai đường trung tuyến ứng với hai cạnh bên bằng nhau.
+ Tổng ba góc trong một tam giác bằng \({180^o}\)
Cách giải:
+ Theo tính chất của tam giác cân thì A, D đúng.
+ Ta có \(\angle A = \angle B = \dfrac{{{{180}^o} – \angle C}}{2} < {90^o}\) . Vậy B đúng.
+ Tam giác ABC cân tại C thì \(AC > AB\)hoặc \(AC \le AB\). Vậy đáp án C sai.
Chọn C.
Câu 6.
Hướng dẫn:
Phân tích dữ liệu biểu đồ đoạn thẳng.
Cách giải:
Từ biểu đồ đoạn thẳng ta thấy lượng mưa tăng giữa các tháng 2 – 3; 3 – 4; 4 – 5; 5 – 6; 7 – 8; 8 – 9.
Chọn B.
Câu 7.
Phương pháp: Giải \({x^2} – 5x = 0\) để tìm nghiệm.
Hướng dẫn giải chi tiết
\({x^2} – 5x = 0 \Rightarrow x(x – 5) = 0 \Rightarrow \left[ \begin{array}{l}x = 0\\x – 5 = 0\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = 0\\x = 5\end{array} \right.\)
Vậy tập nghiệm của đa thức \({x^2} – 5x\)là {0; 5}
Chọn C
Câu 8.
Phương pháp:
– Để trừ hai đa thức, ta nhóm các hạng tử cùng bậc với nhau và rút gọn.
– Thay \(x = – 1\) vào đa thức h(x) vừa tìm được để tìm giá trị của h(x).
Cách giải:
\(\begin{array}{l}h(x) = f(x) – g(x) = \left( { – {x^5} + 2{x^4} – {x^2} – 1} \right) – \left( { – 6 + 2x – 3{x^3} – {x^4} + 3{x^5}} \right)\,\,\,\\\;\;\;\;\;\;\; = – {x^5} + 2{x^4} – {x^2} – 1 + 6 – 2x + 3{x^3} + {x^4} – 3{x^5}\\\;\;\;\;\;\;\; = \left( { – {x^5} – 3{x^5}} \right) + \left( {2{x^4} + {x^4}} \right) + 3{x^3} – {x^2} – 2x + 5\\\;\;\;\;\;\;\; = – 4{x^5} + 3{x^4} + 3{x^3} – {x^2} – 2x + 5.\end{array}\)
Thay \(x = – 1\) vào đa thức h(x) ta có: \(h( – 1) = – 4.{( – 1)^5} + 3.{( – 1)^4} + 3.{( – 1)^3} – {( – 1)^2} – 2.( – 1) + 5 = – 4.( – 1) + 3.1 + 3.( – 1) – 1 + 2 + 5 = 10\)
Vậy giá trị của h(x) là 10 tại \(x = – 1\).
Chọn C
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1.
Hướng dẫn:
Tỉ số phần trăm của a đối với b là: a : b . 100%
Cách giải
a) Sĩ số lớp 7B là:
18 +12 + 3 + 7 = 40 (học sinh).
b) Tỉ lệ phần trăm những bạn có khả năng tự nấu ăn xuất sắc so với sĩ số lớp là:
7 : 40.100 = 17,5
Bài 2.
Hướng dẫn:
a) Thu gọn và sắp xếp theo lũy thừa giảm dần của biến của hai đa thức \(F\left( x \right)\) và \(G\left( x \right)\). Khi thu gọn các đơn thức đồng dạng ta cộng hệ số với nhau và giữ nguyên phần biến, sau đó sắp xếp theo lũy thừa giảm dần của biến số.
b) Tính \(M\left( x \right) = F\left( x \right) – G\left( x \right)\). Ta thực hiện trừ hai đa thức. Sau đó tìm nghiệm của đa thức \(M\left( x \right)\), ta cho \(M\left( x \right) = 0\) để tìm nghiệm.
c) Biến đổi \(N\left( x \right) + F\left( x \right) = – G\left( x \right) \Rightarrow N\left( x \right) = – F\left( x \right) – G\left( x \right)\), rồi thực hiện tính.
Chú ý: Trước dấu trừ các hạng tử đổi dấu.
Cách giải:
a) Thu gọn và sắp xếp theo lũy thừa giảm dần của biến.
Thu gọn \(F\left( x \right):\)
\(\begin{array}{l}F\left( x \right) = 5{x^2} – 1 + 3x + {x^2} – 5{x^3}\\F\left( x \right) = – 5{x^3} + \left( {5{x^2} + {x^2}} \right) + 3x – 1\\F\left( x \right) = – 5{x^3} + 6{x^2} + 3x – 1\end{array}\)
Thu gọn \(G\left( x \right):\)
\(\begin{array}{l}G\left( x \right) = 2 – 3{x^3} + 6{x^2} + 5x – 2{x^3} – x.\\G\left( x \right) = \left( { – 3{x^3} – 2{x^3}} \right) + 6{x^2} + \left( {5x – x} \right) + 2\\G\left( x \right) = – 5{x^3} + 6{x^2} + 4x + 2\end{array}\)
b) Tính \(M\left( x \right)\)
\(\begin{array}{l}M\left( x \right) = F\left( x \right) – G\left( x \right)\\M\left( x \right) = \left( { – 5{x^3} + 6{x^2} + 3x – 1} \right) – \left( { – 5{x^3} + 6{x^2} + 4x + 2} \right)\\M\left( x \right) = – 5{x^3} + 6{x^2} + 3x – 1 + 5{x^3} – 6{x^2} – 4x – 2\\M\left( x \right) = \left( { – 5{x^3} + 5{x^3}} \right) + \left( {6{x^2} – 6{x^2}} \right) + \left( {3x – 4x} \right) + \left( { – 1 – 2} \right)\\M\left( x \right) = \,\, – x – 3\end{array}\)
Tìm nghiệm của đa thức \(M\left( x \right)\):
Ta có: \(M\left( x \right) = – x – 3 = 0 \Leftrightarrow x = – 3\)
Vậy \(x = – 3\) là nghiệm của đa thức \(M\left( x \right)\).
c) Ta có:
\(\begin{array}{l}N\left( x \right) + F\left( x \right) = – G\left( x \right)\\ \Rightarrow N\left( x \right) = – F\left( x \right) – G\left( x \right) = – \left[ {F\left( x \right) + G\left( x \right)} \right]\end{array}\)
Trong đó:
\(F\left( x \right) = – 5{x^3} + 6{x^2} + 3x – 1\)
\(G\left( x \right) = – 5{x^3} + 6{x^2} + 4x + 2\)
\(\begin{array}{l} \Rightarrow F\left( x \right) + G\left( x \right)\\ = \left( { – 5{x^3} + 6{x^2} + 3x – 1} \right) + \left( { – 5{x^3} + 6{x^2} + 4x + 2} \right)\\ = – 10{x^3} + 12{x^2} + 7x + 1\end{array}\)
\(\begin{array}{l} \Rightarrow N\left( x \right) = – \left[ {F\left( x \right) + G\left( x \right)} \right]\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = – \left( { – 10{x^3} + 12{x^2} + 7x + 1} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 10{x^3} – 12{x^2} – 7x – 1\end{array}\)
Vậy \(N\left( x \right) = 10{x^3} – 12{x^2} – 7x – 1\).
Câu 3:
Hướng dẫn:
+ Sử dụng các cách chứng minh hai tam giác bằng nhau.
+ Sử dụng tính chất của các góc tạo bởi một đường thẳng cắt hai đường thẳng song song.
+ Các định lí từ vuông góc tới song song.
+ Tính chất các đường cao, đường phân giác, đường trung trực trong tam giác cân.
Cách giải:
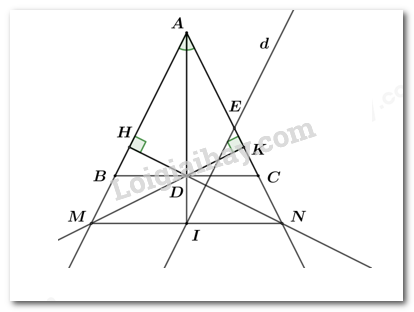
a) Xét hai tam giác vuông\(\Delta AHD\)và\(\Delta AKD\)có:
+ \(AD\)chung
+ \(\angle HAD = \angle KAD\) (vì\(AD\)là tia phân giác của \(\angle BAC\))
\( \Rightarrow \Delta AHD = \)\(\Delta AKD\) (cạnh huyền – góc nhọn) (đpcm)
b) Theo a) \(\Delta AHD = \)\(\Delta AKD\)\( \Rightarrow \)\(AH = AK\)(hai cạnh tương ứng) (1)
Xét hai tam giác vuông\(\Delta AMK\)và\(\Delta ANH\)có:
+ \(\angle A\)chung
+\(AH = AK\)
+ \(\angle AKM = \angle AHN = {90^o}\)
\( \Rightarrow \)\(\Delta AMK = \Delta ANH\)(g.c.g)
\( \Rightarrow \)\(AM = AN\) (2)
Mà \(\begin{array}{l}AM = AH + HM\\AN = AK + KN\end{array}\) (3)
Từ (1), (2), (3) suy ra \(HM = KN\) (đpcm)
c) + Do \(AM = AN\)\( \Rightarrow \Delta AMN\)cân tại \(A\)
Vì \(AD\)là tia phân giác của góc \(A\)nên suy ra \(AD\)đồng thời là đường cao trong \(\Delta AMN\)ứng với cạnh \(MN\).
\( \Rightarrow AD \bot MN\) (đpcm). (4)
+ \(\Delta ABC\)có \(AD\)là tia phân giác của góc \(A\)nên suy ra \(AD\)đồng thời là đường cao ứng với cạnh \(BC\).
\( \Rightarrow AD \bot BC\) (5)
Từ (4), (5) suy ra \(MN//BC\) (đpcm)
d) + Đường thẳng d song song với \(AM\)
\( \Rightarrow \)\(\angle AMN = \angle EIN\)(hai góc ở vị trí so le trong) (7)
Mặt khác \(\Delta AMN\)cân tại \(A\)\( \Rightarrow \)\(\angle AMN = \angle ANM\) (8)
Từ (7) và (8) suy ra: \(\angle EIN = \angle ANM = \angle ENI\)
\( \Rightarrow \)\(\Delta ENI\)cân tại \(E\)
\( \Rightarrow \)\(EI = EN\) (9)
+ Đường thẳng d song song với \(AM\)
\( \Rightarrow \)\(\angle EIA = \angle MAI{\rm{ }}\left( { = \angle AIE} \right)\)
\( \Rightarrow \)\(\Delta EAI\)cân tại \(E\)
\( \Rightarrow \)\(EI = EA\) (10)
Từ (9) và (10) suy ra: \(EI = EN = EA = \dfrac{1}{2}AN = \dfrac{1}{2}AM \Leftrightarrow EI = \dfrac{1}{2}AM\) (đpcm)
Bài 4.
Hướng dẫn:
Xét với \(x = – 1\), ta tìm được mối liên hệ của \(f\left( { – 1} \right)\) và \(f\left( 1 \right)\)
Xét với \(x = 1\), ta tìm được \(f\left( 1 \right)\).
Cách giải:
+ Với \(x = – 1\), ta có: \(f\left( { – 1} \right) + \left( { – 1} \right).f\left( 1 \right) = – 1 + 1\)
\(\begin{array}{l} \Rightarrow f\left( { – 1} \right) – f\left( 1 \right) = 0\\ \Rightarrow f\left( { – 1} \right) = f\left( 1 \right)\end{array}\)
+ Với \(x = 1\), ta có: \(f\left( 1 \right) + 1.f\left( { – 1} \right) = 1 + 1\)
\( \Rightarrow f\left( 1 \right) + f\left( { – 1} \right) = 2\)
Suy ra, \(f\left( 1 \right) + f\left( 1 \right) = 2\)
\(\begin{array}{l} \Rightarrow 2f\left( 1 \right) = 2\\ \Rightarrow f\left( 1 \right) = 1\end{array}\)
Vậy \(f\left( 1 \right) = 1\).