Trả lời Câu hỏi Vận dụng 5 trang 39 SGK Toán 12 Kết nối tri thức – Bài 14. Phương trình mặt phẳng. Gợi ý: Sử dụng kiến thức về khoảng cách từ một điểm đến một mặt phẳng để tính: Trong không gian Oxyz.
Câu hỏi/Đề bài:
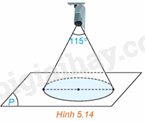
Góc quan sát ngang của một camera là \({115^0}\). Trong không gian Oxyz, camera được đặt tại điểm C(1; 2; 4) và chiếu thẳng về phía mặt phẳng \(\left( P \right):x + 2y + 2z + 3 = 0\). Hỏi vùng quan sát được trên mặt phẳng (P) của camera là hình tròn có bán kính bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất).
Hướng dẫn:
Sử dụng kiến thức về khoảng cách từ một điểm đến một mặt phẳng để tính: Trong không gian Oxyz, khoảng cách từ điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):Ax + By + Cz + D = 0\) là \(d\left( {M,\left( P \right)} \right) = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).
Lời giải:
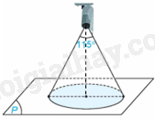
Khoảng cách từ điểm C đến mặt phẳng (P) là: \(d\left( {C,\left( P \right)} \right) = \frac{{\left| {1.1 + 2.2 + 2.4 + 3} \right|}}{{\sqrt {{1^2} + {2^2} + {2^2}} }} = \frac{{16}}{3}\)
Vùng quan sát trên mặt phẳng (P) của camera là hình tròn có bán kính là:
\(R = d\left( {C,\left( P \right)} \right).\tan \frac{{{{115}^0}}}{2} \approx 8,4\)