Lời giải Câu hỏi Hoạt động 6 trang 52 SGK Toán 12 Kết nối tri thức – Bài 6. Vectơ trong không gian. Gợi ý: Sử dụng kiến thức về hai vectơ cùng phương để chứng minh.
Câu hỏi/Đề bài:
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của AB, AC (H.2.17)
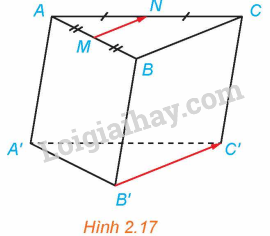
a) Hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {B’C’} \) có cùng phương không? Có cùng hướng không?
b) Giải thích vì sao \(\left| {\overrightarrow {MN} } \right| = \frac{1}{2}\left| {\overrightarrow {B’C’} } \right|\).
Hướng dẫn:
a) Sử dụng kiến thức về hai vectơ cùng phương để chứng minh: Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
b) Sử dụng kiến thức về độ dài của vectơ trong không gian để chứng minh: Độ dài của vectơ trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Độ dài của vectơ \(\overrightarrow a \) được kí hiệu là \(\left| {\overrightarrow a } \right|\).
Lời giải:
a) Vì MN là đường trung bình của tam giác ABC nên MN//BC.
Vì BCC’B’ là hình bình hành nên BC//B’C’. Suy ra: MN//B’C’.
Do đó hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {B’C’} \) có cùng phương và cùng hướng.
b) Vì BCC’B’ là hình bình hành nên \(BC = B’C’\)
Vì MN là đường trung bình của tam giác ABC nên \(MN = \frac{1}{2}BC\)
Suy ra: \(\left| {\overrightarrow {MN} } \right| = \frac{1}{2}\left| {\overrightarrow {B’C’} } \right|\).