Câu hỏi Hoạt động 6 trang 46 Toán 12 Kết nối tri thức: Trong không gian Oxyz, cho hai đường thẳng Δ _1, Δ _2 lần lượt đi qua các điểm A_1 x_1;y_1;z_1, A_2 x_2;y_2;z_2

Câu hỏi/Đề bài:

Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({A_1}\left( {{x_1};{y_1};{z_1}} \right),{A_2}\left( {{x_2};{y_2};{z_2}} \right)\) và tương ứng có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right),\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\). (H.5.29).

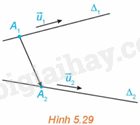
a) Tìm điều kiện đối với \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) để \({\Delta _1}\) và \({\Delta _2}\) song song hoặc trùng nhau.

b) Giả sử \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \) và \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = 0\) thì \({\Delta _1}\) và \({\Delta _2}\) có cắt nhau hay không?

c) Giả sử \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne 0\) thì \({\Delta _1}\) và \({\Delta _2}\) có chéo nhau hay không?

Hướng dẫn:

Sử dụng kiến thức về giá của vectơ trong không gian để tìm chứng minh: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ.

Lời giải:

a) Để \({\Delta _1}\) và \({\Delta _2}\) song song hoặc trùng nhau thì giá của hai vectơ \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) song song hoặc trùng nhau. Suy ra, \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) cùng phương.

b) Vì \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \) mà \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = 0\) nên \(\overrightarrow {{A_1}{A_2}} = \overrightarrow 0 \), suy ra \({A_1}\) trùng \({A_2}\). Do đó, \({\Delta _1}\) và \({\Delta _2}\) cắt nhau.

c) Vì \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne 0\) nên \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \) và \(\overrightarrow {{A_1}{A_2}} \ne \overrightarrow 0 \) nên \({\Delta _1}\) và \({\Delta _2}\) chéo nhau.