Trả lời Câu hỏi Hoạt động 2 trang 17 SGK Toán 12 Kết nối tri thức – Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số. Tham khảo: Sử dụng kiến thức về khái niệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số để tính.
Câu hỏi/Đề bài:
Xét hàm số \(y = f\left( x \right) = {x^3} – 2{x^2} + 1\) trên đoạn \(\left[ { – 1;2} \right]\), với đồ thị như Hình 1.16.
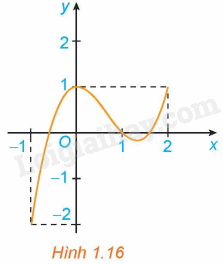
a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \(\left[ { – 1;2} \right]\).
b) Tính đạo hàm f’(x) và tìm các điểm \(x \in \left( { – 1;2} \right)\) mà \(f’\left( x \right) = 0\).
c) Tính giá trị của hàm số tại hai đầu mút của đoạn \(\left[ { – 1;2} \right]\) và tại các điểm x đã tìm ở câu b. So sánh số nhỏ nhất trong các giá trị này với \(\mathop {\min }\limits_{\left[ { – 1;2} \right]} f\left( x \right)\), số lớn nhất trong các giá trị này với \(\mathop {\max }\limits_{\left[ { – 1;2} \right]} f\left( x \right)\).
Hướng dẫn:
Sử dụng kiến thức về khái niệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số để tính: Cho hàm số \(y = f\left( x \right)\) xác định trên tập D.
+ Số M được gọi là giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trên tập D nếu \(f\left( x \right) \le M\) với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f\left( {{x_0}} \right) = M\).
Kí hiệu \(M = \mathop {\max }\limits_{x \in D} f\left( x \right)\) hoặc \(M = \mathop {\max }\limits_D f\left( x \right)\)
+ Số m được gọi là giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên tập D nếu \(f\left( x \right) \ge m\) với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f\left( {{x_0}} \right) = m\).
Kí hiệu \(m = \mathop {\min }\limits_{x \in D} f\left( x \right)\) hoặc \(m = \mathop {\min }\limits_D f\left( x \right)\)
Lời giải:
a) Nhìn vào đồ thị ta thấy, trên đoạn \(\left[ { – 1;2} \right]\) ta có:
+ Giá trị lớn nhất của hàm số là \(\mathop {\max }\limits_{\left[ { – 1;2} \right]} f\left( x \right) = f\left( 0 \right) = f\left( 2 \right) = 1\).
+ Giá trị nhỏ nhất của hàm số là \(\mathop {\min }\limits_{\left[ { – 1;2} \right]} f\left( x \right) = f\left( { – 1} \right) = – 2\).
b) \(f’\left( x \right) = 3{x^2} – 4x,f’\left( x \right) = 0 \Leftrightarrow 3{x^2} – 4x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \frac{4}{3}\end{array} \right.\)
Vậy \(x = 0,x = \frac{4}{3}\) thì \(f’\left( x \right) = 0\).
c) Ta có: \(f\left( 0 \right) = 1;f\left( {\frac{4}{3}} \right) = {\left( {\frac{4}{3}} \right)^3} – 2.{\left( {\frac{4}{3}} \right)^2} + 1 = \frac{{ – 5}}{{27}};f\left( { – 1} \right) = {\left( { – 1} \right)^3} – 2.{\left( { – 1} \right)^2} + 1 = – 2\);
\(f\left( 2 \right) = {2^3} – {2.2^2} + 1 = 1\)
Do đó, số nhỏ nhất trong các giá trị này là \( – 2\), số lớn nhất trong các giá trị này là 1.
Ta thấy: \(\mathop {\max }\limits_{\left[ { – 1;2} \right]} f\left( x \right) = 1\), \(\mathop {\min }\limits_{\left[ { – 1;2} \right]} f\left( x \right) = – 2\).