Sử dụng kiến thức về dạng của đồ thị hàm số để chọn đáp án. Lời giải bài tập, câu hỏi Giải bài tập 4 trang 90 SGK Toán 12 tập 2 – Kết nối tri thức – Bài tập ôn tập cuối năm. Đường cong trong hình bên là đồ thị của một trong bốn hàm số dưới đây….
Đề bài/câu hỏi:
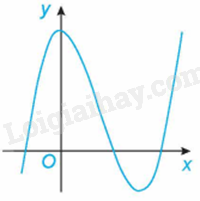
Đường cong trong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
A. \(y = – {x^3} + 3{x^2} + 1\).
B. \(y = {x^3} – 3{x^2} + 3\).
C. \(y = – {x^2} + 2x + 1\).
D. \(y = \frac{{x + 1}}{{x – 1}}\).
Hướng dẫn:
Sử dụng kiến thức về dạng của đồ thị hàm số để chọn đáp án.
Lời giải:
Đây là là dạng của đồ thị hàm số bậc ba nên đáp án C, D sai.
Đồ thị hàm số trong hình vẽ đồng biến trên khoảng \(\left( { – \infty ;0} \right)\).
Xét hàm số: \(y = {x^3} – 3{x^2} + 3\) ta có: \(y’ = 3{x^2} – 6x,y’ = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)
Do đó, hàm số \(y = {x^3} – 3{x^2} + 3\) đồng biến trên khoảng \(\left( { – \infty ;0} \right)\).
Chọn B