Sử dụng kiến thức về phương sai của mẫu số liệu ghép nhóm để tính: Phương sai của mẫu số liệu ghép nhóm. Trả lời Giải bài tập 3.7 trang 84 SGK Toán 12 tập 1 – Kết nối tri thức – Bài 10. Phương sai và độ lệch chuẩn. Thời gian chạy tập luyện cự li 100m của hai vận động viên được cho trong bảng sau:…
Đề bài/câu hỏi:
Thời gian chạy tập luyện cự li 100m của hai vận động viên được cho trong bảng sau: 
Dựa trên độ lệch chuẩn của mẫu số liệu ghép nhóm, hãy cho biết vận động viên nào có thành tích luyện tập ổn định hơn.
Hướng dẫn:
a) Sử dụng kiến thức về phương sai của mẫu số liệu ghép nhóm để tính: Phương sai của mẫu số liệu ghép nhóm, kí hiệu là \({s^2}\), là một số được tính theo công thức sau: \({s^2} = \frac{1}{n}\left( {{m_1}x_1^2 + … + {m_k}x_k^2} \right) – {\left( {\overline x } \right)^2}\), trong đó \(n = {m_1} + … + {m_k}\) với \(\overline x = \frac{{{m_1}{x_1} + … + {m_k}{x_k}}}{n}\) là số trung bình của mẫu số liệu ghép nhóm.
Sử dụng kiến thức độ lệch chuẩn của mẫu số liệu ghép nhóm để tính: Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} \)
b) Sử dụng kiến thức về ý nghĩa của độ lệch chuẩn để nhận xét: Độ lệch chuẩn dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu đó. Độ lệch chuẩn càng lớn thì mẫu số liệu càng phân tán.
Lời giải:
Ta có bảng số liệu với giá trị đại diện: 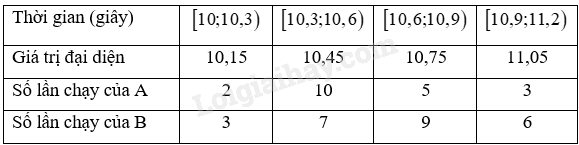
Vận động viên A:
Giá trị trung bình \(\overline {{x_A}} = \frac{{10,15.2 + 10,45.10 + 10,75.5 + 11,05.3}}{{2 + 10 + 5 + 3}} = \frac{{2117}}{{200}}\)
Phương sai: \(s_A^2 = \frac{1}{{20}}\left( {10,{{15}^2}.2 + 10,{{45}^2}.10 + 10,{{75}^2}.5 + 11,{{05}^2}.3} \right) – {\left( {\frac{{2117}}{{200}}} \right)^2} = \frac{{2691}}{{40000}}\)
Độ lệch chuẩn: \({s_A} = \sqrt {\frac{{2691}}{{40000}}} \approx 0,26\)
Vận động viên B:
Giá trị trung bình \(\overline {{x_B}} = \frac{{10,15.3 + 10,45.7 + 10,75.9 + 11,05.6}}{{3 + 7 + 9 + 6}} = \frac{{5333}}{{500}}\)
Phương sai: \(s_B^2 = \frac{1}{{25}}\left( {10,{{15}^2}.3 + 10,{{45}^2}.7 + 10,{{75}^2}.9 + 11,{{05}^2}.6} \right) – {\left( {\frac{{5333}}{{500}}} \right)^2} = \frac{{1296}}{{15625}}\)
Độ lệch chuẩn: \({s_B} = \sqrt {\frac{{1296}}{{15625}}} = 0,288\)
Vì \({s_A} < {s_B}\) nên vận động viên A có thành tích luyện tập ổn định hơn.