Sử dụng kiến thức về phương sai của mẫu số liệu ghép nhóm để tính: Phương sai của mẫu số liệu ghép nhóm. Phân tích, đưa ra lời giải Giải bài tập 3.4 trang 84 SGK Toán 12 tập 1 – Kết nối tri thức – Bài 10. Phương sai và độ lệch chuẩn. Kiểm tra khối lượng của 30 bao xi măng (đơn vị:…
Đề bài/câu hỏi:
Kiểm tra khối lượng của 30 bao xi măng (đơn vị: kg) được chọn ngẫu nhiên trước khi xuất xưởng cho kết quả như sau:

a) Thay dấu “?” bằng số thích hợp để hoàn thiện mẫu số liệu ghép nhóm sau.

b) Tìm phương sai và độ lệch chuẩn của mẫu số liệu gốc và mẫu số liệu ghép nhóm. Giá trị nào là giá trị chính xác? Giá trị nào là giá trị xấp xỉ?
Hướng dẫn:
Sử dụng kiến thức về phương sai của mẫu số liệu ghép nhóm để tính: Phương sai của mẫu số liệu ghép nhóm, kí hiệu là \({s^2}\), là một số được tính theo công thức sau: \({s^2} = \frac{1}{n}\left( {{m_1}x_1^2 + … + {m_k}x_k^2} \right) – {\left( {\overline x } \right)^2}\), trong đó \(n = {m_1} + … + {m_k}\) với \(\overline x = \frac{{{m_1}{x_1} + … + {m_k}{x_k}}}{n}\) là số trung bình của mẫu số liệu ghép nhóm.
Sử dụng kiến thức độ lệch chuẩn của mẫu số liệu ghép nhóm để tính: Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} \)
Lời giải:
a) Hoàn thành bảng:

b) Với mẫu số liệu gốc:
+ Giá trị trung bình là: \(\overline x = (49,5 + 48,9 + 51,4 + 51,1 + 49,3 + 48,7 + 50,8 + 50,7 + 51,2 + \)
\( + 50,2 + 48,8 + 50,6 + 48,7 + 49,8 + 50,9 + 49,6 + 48,8 + 49,2 + 51,3 + 51,2 + 50,7 + 51,4 + \)
\( + 50,4 + 51,1 + 50,1 + 50,0 + 48,6 + 50,5 + 51,2 + 49,6).\frac{1}{{30}} = \frac{{15043}}{{300}}\)
+ Phương sai: 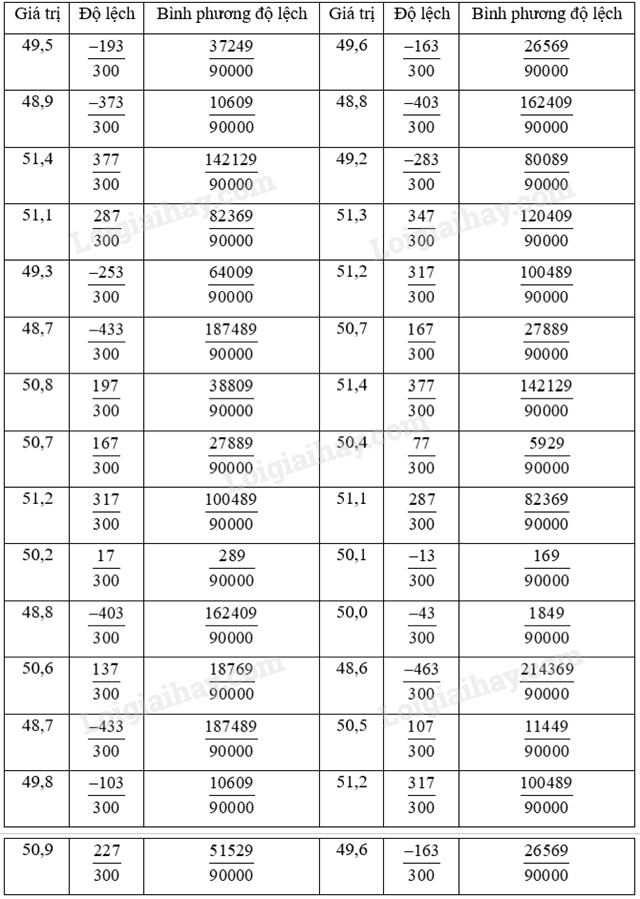
Tổng bình phương độ lệch: \(\frac{{78461}}{{3000}}\)
Phương sai: \({s^2} = \frac{1}{{30}}.\frac{{78461}}{{3000}} = \frac{{78461}}{{90000}}\)
Độ lệch chuẩn: \[s = \sqrt {{s^2}} = \frac{{\sqrt {78461} }}{{300}} \approx 0,934\]
Theo mẫu số liệu ghép nhóm:
Ta có bảng số liệu với giá trị đại diện:
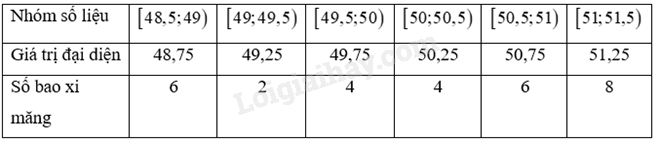
Giá trị trung bình: \(\overline x = \frac{{48,75.6 + 49,25.2 + 49,75.4 + 50,25.4 + 50,75.6 + 51,25.8}}{{30}} = \frac{{3011}}{{60}}\)
Phương sai:
\({s^2} = \frac{1}{{30}}\left( {48,{{75}^2}.6 + 49,{{25}^2}.2 + 49,{{75}^2}.4 + 50,{{25}^2}.4 + 50,{{75}^2}.6 + 51,{{25}^2}.8} \right) – {\left( {\frac{{3011}}{{60}}} \right)^2} = \frac{{194}}{{225}}\)
Độ lệch chuẩn: \(s = \sqrt {{s^2}} \approx 0,929\)
Giá trị tính từ mẫu số liệu gốc là chính xác, giá trị tính từ mẫu số liệu ghép nhóm là giá trị xấp xỉ.