Sử dụng kiến thức về cách tìm cực trị của hàm số để tìm cực trị của hàm số \(y = f\left( x \right)\): 1. Phân tích, đưa ra lời giải Giải bài tập 1.7 trang 14 SGK Toán 12 tập 1 – Kết nối tri thức – Bài 1. Tính đơn điệu và cực trị của hàm số. Tìm cực trị của các hàm số sau: a) \(y = 2{x^3} – 9{x^2} + 12x – 5\);…
Đề bài/câu hỏi:
Tìm cực trị của các hàm số sau:a) \(y = 2{x^3} – 9{x^2} + 12x – 5\);\(y = {x^4} – 4{x^2} + 2\)b) ;c) \(y = \frac{{{x^2} – 2x + 3}}{{x – 1}}\);d) \(y = \sqrt {4x – 2{x^2}} \).
Hướng dẫn:
Sử dụng kiến thức về cách tìm cực trị của hàm số để tìm cực trị của hàm số \(y = f\left( x \right)\):
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.
3. Lập bảng biến thiên của hàm số.
4. Từ bảng biến thiên suy ra các cực trị của hàm số.
Lời giải:
a) Tập xác định: \(D = \mathbb{R}\).
\(y’ = 6{x^2} – 18x + 12\), \(y’ = 0 \Leftrightarrow 6{x^2} – 18x + 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\)
Bảng biến thiên:
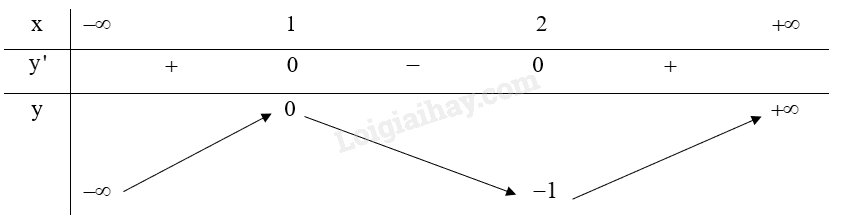
Từ bảng biến thiên ta có:
Hàm số \(y = 2{x^3} – 9{x^2} + 12x – 5\) có điểm cực đại là \(\left( {1;0} \right)\).
Hàm số \(y = 2{x^3} – 9{x^2} + 12x – 5\) có điểm cực tiểu là \(\left( {2; – 1} \right)\).
b) Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \(y’ = 4{x^3} – 8x,y’ = 0 \Leftrightarrow 4{x^3} – 8x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 2 \end{array} \right.\)
Bảng biến thiên:
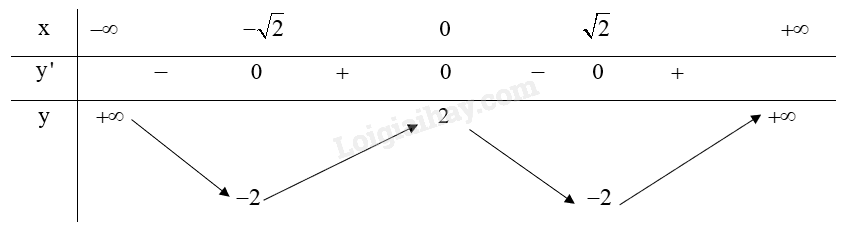
Từ bảng biến thiên ta có:
Hàm số \(y = {x^4} – 4{x^2} + 2\) đạt cực đại tại \(x = 0\) và .
Hàm số \(y = {x^4} – 4{x^2} + 2\) đạt cực tiểu tại \(x = \pm \sqrt 2 \) và \({y_{CT}} = – 2\).
c) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).
Ta có: \(y’ = \frac{{\left( {2x – 2} \right)\left( {x – 1} \right) – \left( {{x^2} – 2x + 3} \right)}}{{{{\left( {x – 1} \right)}^2}}} = \frac{{{x^2} – 2x – 1}}{{{{\left( {x – 1} \right)}^2}}}\)
\(y’ = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 – \sqrt 2 \\x = 1 + \sqrt 2 \end{array} \right.\) (thỏa mãn)
Lập bảng biến thiên của hàm số:
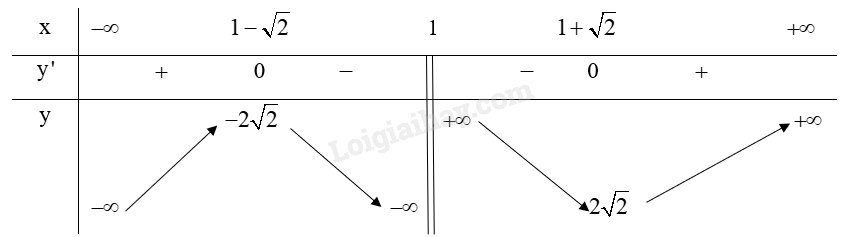
Từ bảng biến thiên ta có:
Hàm số \(y = \frac{{{x^2} – 2x + 3}}{{x – 1}}\) đạt cực đại tại \(x = 1 – \sqrt 2 \) và .
Hàm số \(y = \frac{{{x^2} – 2x + 3}}{{x – 1}}\) đạt cực tiểu tại \(x = 1 + \sqrt 2 \) và \({y_{CT}} = 2\sqrt 2 \).
d) \(y = \sqrt {4x – 2{x^2}} \)
Tập xác định: \(D = \left[ {0;2} \right]\).
Ta có: \(y’ = \frac{{\left( {4x – 2{x^2}} \right)’}}{{2\sqrt {4x – 2{x^2}} }} = \frac{{ – x + 1}}{{\sqrt {4x – 2{x^2}} }},y’ = 0 \Leftrightarrow x = 1\left( {tm} \right)\)
Ta có bảng biến thiên của hàm số:
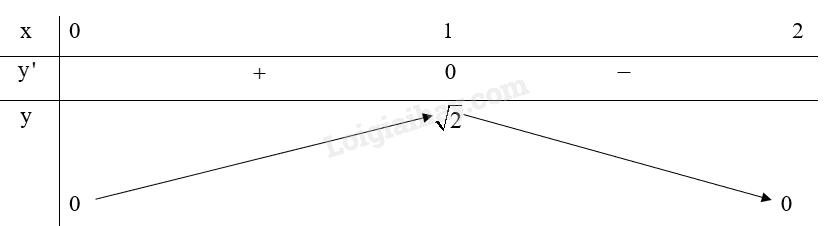
Do đó, hàm số đạt cực đại tại \(x = 1\), , hàm số không có cực tiểu.