Đáp án Câu hỏi Vận dụng 6 trang 42 SGK Toán 12 Chân trời sáng tạo – Giải mục 5 trang 41 – 42 SGK Toán 12 tập 2. Tham khảo: Xác định toạ độ các điểm \(C\), \(S\), \(A\), \(B\), sau đó viết phương trình mặt phẳng \(\left( {SAB} \right)\.
Câu hỏi/Đề bài:
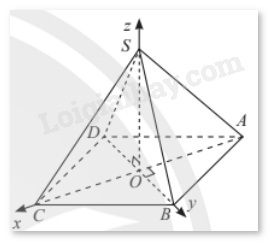
Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\sqrt 2 \), chiều cao bằng \(2a\) và \(O\) là tâm của đáy. Bằng cách thiết lập hệ trục toạ độ \(Oxyz\) như hình dưới đây, tính khoảng cách từ điểm \(C\) đến mặt phẳng \(\left( {SAB} \right)\).
Hướng dẫn:
Xác định toạ độ các điểm \(C\), \(S\), \(A\), \(B\), sau đó viết phương trình mặt phẳng \(\left( {SAB} \right)\) rồi sử dụng công thức tính khoảng cách để tính khoảng cách từ điểm \(C\) đến mặt phẳng \(\left( {SAB} \right)\).
Lời giải:
Hình vuông \(ABCD\) có cạnh \(a\sqrt 2 \), nên đường chéo có độ dài \(\sqrt {{{\left( {a\sqrt 2 } \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}} = 2a\). Suy ra \(OA = OB = OC = \frac{{2a}}{2} = a\).
Chiều cao của hình chóp đều là \(2a\), nên \(SO = 2a\)
Điểm \(A\) nằm trên trục \(Ox\), \(OA = a\) và \({x_A} < 0\) nên ta có \(A\left( { – a;0;0} \right)\).
Điểm \(B\) nằm trên trục \(Oy\), \(OB = a\) và \({y_B} > 0\) nên ta có \(B\left( {0;a;0} \right)\).
Điểm \(C\) nằm trên trục \(Ox\), \(OC = a\) và \({x_C} > 0\) nên ta có \(C\left( {a;0;0} \right)\).
Điểm \(S\) nằm trên trục \(Oz\), \(OS = 2a\) và \({z_S} > 0\) nên ta có \(S\left( {0;0;2a} \right)\).
Mặt phẳng \(\left( {SAB} \right)\) đi qua \(A\left( { – a;0;0} \right)\), \(B\left( {0;a;0} \right)\), \(S\left( {0;0;2a} \right)\) nên có phương trình là \(\frac{x}{{ – a}} + \frac{y}{a} + \frac{z}{{2a}} = 1 \Leftrightarrow – 2x + 2y + z = 2a \Leftrightarrow – 2x + 2y + z – 2a = 0\).
Khoảng cách từ \(C\left( {a;0;0} \right)\) đến mặt phẳng \(\left( {SAB} \right)\) là:
\(d\left( {C,\left( {SAB} \right)} \right) = \frac{{\left| { – 2.a + 2.0 + 0 – 2a} \right|}}{{\sqrt {{{\left( { – 2} \right)}^2} + {2^2} + {1^2}} }} = \frac{{4a}}{3}\)