Lời giải Câu hỏi Vận dụng 2 trang 56 SGK Toán 12 Chân trời sáng tạo – Bài 2. Toạ độ của vectơ trong không gian. Tham khảo: Áp dụng hệ thức về cạnh và góc trong các tam giác vuông để tìm hoành độ, tung độ.
Câu hỏi/Đề bài:
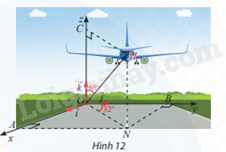
Một máy bay đang cất cánh từ phi trường. Với hệ toạ độ Oxyz được thiết lập như Hình 12, cho biết M là vị trí của máy bay, OM = 14, \(\widehat {NOB} = 32^\circ \), \(\widehat {MOC} = 65^\circ \). Tìm toạ độ điểm M.
Hướng dẫn:
Áp dụng hệ thức về cạnh và góc trong các tam giác vuông để tìm hoành độ, tung độ, cao độ của M
Lời giải:
Xét tam giác COM vuông tại C:
\(CO = OM.\cos 65^\circ = 14.\cos 65^\circ \approx 5,92\)
\(CM = OM.\sin 65^\circ = 14.\sin 65^\circ \approx 12,69\)
Xét tam giác BON vuông tại B:
\(OB = ON.\cos 32^\circ = CM.\cos 32^\circ = 12,69.\cos 32^\circ \approx 10,76\)
Xét tam giác AON vuông tại A:
\(OA = ON.\cos (90^\circ – 32^\circ ) = 12,69.\cos 58^\circ = 6,72\)
Vậy tọa độ của M là (6,72; 10,76; 5,92)