Giải chi tiết Câu hỏi Vận dụng 1 trang 24 SGK Toán 12 Chân trời sáng tạo – Bài 3. Ứng dụng hình học của tích phân. Tham khảo: Ta ghép mặt cắt của cửa hầm vào mặt phẳng \(Oxy\) như hình vẽ dưới đây.
Câu hỏi/Đề bài:
Mặt cắt của một cửa hầm có dạng là hình phẳng giới hạn bởi một parabol và đường thẳng nằm ngang như hình 7. Tính diện tích của cửa hầm.
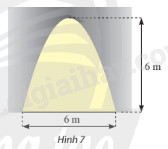
Hướng dẫn:
Ta ghép mặt cắt của cửa hầm vào mặt phẳng \(Oxy\) như hình vẽ dưới đây.
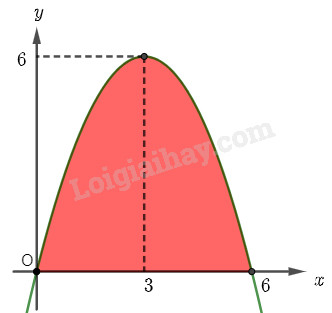
Diện tích của cửa hầm chính là diện tích phần mặt phẳng giới hạn bởi parabol \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = 0\) và \(x = 6\).
Để tính được diện tích của cửa hầm, ta xác định phương trình của parabol \(y = f\left( x \right)\) như trong hình, sau đó tính tích phân \(S = \int\limits_0^6 {\left| {f\left( x \right)} \right|dx} \).
Lời giải:
Ta ghép mặt cắt của cửa hầm vào mặt phẳng \(Oxy\) như hình vẽ dưới đây. Diện tích của cửa hầm chính là diện tích hình phẳng giới hạn bởi parabol \(y = f\left( x \right) = a{x^2} + bx + c\), trục hoành và hai đường thẳng \(x = 0\), \(x = 6\).
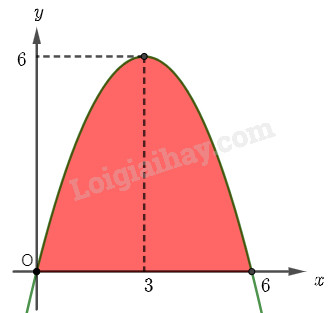
Ta nhận thấy rằng parabol đi qua các điểm có toạ độ \(\left( {0;0} \right)\), \(\left( {6;0} \right)\) và \(\left( {3;6} \right)\) (trục đối xứng của parabol đi qua đỉnh), do đó ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{a{{.0}^2} + b.0 + c = 0}\\{a{{.6}^2} + b.6 + c = 0}\\{a{{.3}^2} + b.3 + c = 6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{c = 0}\\{36a + 6b + c = 0}\\{9a + 3b + c = 6}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = – \frac{2}{3}}\\{b = 4}\\{c = 0}\end{array}} \right.} \right.\)
Vậy phương trình của parabol là \(y = – \frac{2}{3}{x^2} + 4x\).
Ta thấy rằng với \(x \in \left[ {0;6} \right]\) thì parabol nằm trên trục hoành. Do đó, diện tích của cửa hầm, cũng chính là diện tích hình phẳng giới hạn bởi parabol \(y = – \frac{2}{3}{x^2} + 4x\), trục hoành và các đường thẳng \(x = 0\), \(x = 6\) là:
\(S = \int\limits_0^6 {\left| { – \frac{2}{3}{x^2} + 4x} \right|dx} = \int\limits_0^6 {\left( { – \frac{2}{3}{x^2} + 4x} \right)dx} = \left. {\left( {\frac{{ – 2}}{9}{x^3} + 2{x^2}} \right)} \right|_0^6 = 24\)
Vậy diện tích của cửa hầm là 24 \({{\rm{m}}^2}\).