Hướng dẫn giải Câu hỏi Hoạt động 1 trang 61 SGK Toán 12 Chân trời sáng tạo – Giải mục 1 trang 61 – 62 – 63 SGK Toán 12 tập 2. Tham khảo: Sử dụng công thức tính khoảng cách giữa hai điểm trong không gian để tính khoảng cách \(IM\).
Câu hỏi/Đề bài:
Trong không gian \(Oxyz\), cho mặt cầu \(S\left( {I;R} \right)\) có tâm \(I\left( {a;b;c} \right)\) và bán kính \(R\). Xét một điểm \(M\left( {x;y;z} \right)\) thay đổi.
a) Tính khoảng cách \(IM\) theo \(x\), \(y\), \(z\) và \(a\), \(b\), \(c\).
b) Nêu điều kiện cần và đủ của \(x\), \(y\), \(z\) để điểm \(M\left( {x;y;z} \right)\) nằm trên mặt cầu \(S\left( {I;R} \right)\).
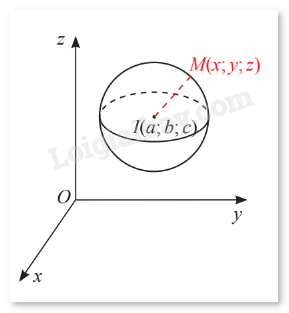
Hướng dẫn:
a) Sử dụng công thức tính khoảng cách giữa hai điểm trong không gian để tính khoảng cách \(IM\).
b) Để điểm \(M\) nằm trên mặt cầu \(S\left( {I;R} \right)\) thì \(IM = R\).
Lời giải:
a) Ta có \(I\left( {a;b;c} \right)\) và \(M\left( {x;y;z} \right)\). Suy ra \(IM = \sqrt {{{\left( {x – a} \right)}^2} + {{\left( {y – b} \right)}^2} + {{\left( {z – c} \right)}^2}} \).
b) Điều kiện cần và đủ của \(x\), \(y\), \(z\) để điểm \(M\left( {x;y;z} \right)\) nằm trên mặt cầu \(S\left( {I;R} \right)\) là \(IM = R\), điều này tương đương với
\(\sqrt {{{\left( {x – a} \right)}^2} + {{\left( {y – b} \right)}^2} + {{\left( {z – c} \right)}^2}} = R \Leftrightarrow {\left( {x – a} \right)^2} + {\left( {y – b} \right)^2} + {\left( {z – c} \right)^2} = {R^2}\).