Trả lời Câu hỏi Hoạt động 3 trang 9 SGK Toán 12 Cánh diều – Bài 1. Tính đơn điệu của hàm số. Gợi ý: Dựa vào đồ thị hàm số.
Câu hỏi/Đề bài:
Dựa vào đồ thị hàm số \(y = f\left( x \right) = – {x^3} – 3{x^2} + 3\) ở Hình 3, hãy so sánh:
a) \(f\left( { – 2} \right)\) với mỗi giá trị \(f\left( x \right)\), ở đó \(x \in \left( { – 3; – 1} \right)\) và \(x \ne – 2\).
b) \(f\left( 0 \right)\)với mỗi giá trị \(f\left( x \right)\), ở đó \(x \in \left( { – 1;1} \right)\) và \(x \ne 0\).
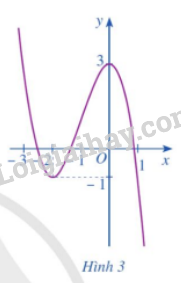
Hướng dẫn:
Dựa vào đồ thị hàm số
Lời giải:
a) Nhận xét: Ta thấy rằng \(f\left( x \right) > f\left( { – 2} \right)\) với mọi \(x \in \left( { – 3; – 1} \right)\) và \(x \ne – 2\).
b) Tương tự: Ta thấy rằng \(f\left( x \right) < f\left( 0 \right)\) với mọi \(x \in \left( { – 1;1} \right)\) và \(x \ne 0\).